题目内容

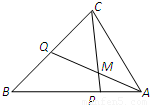
在△ABC中，点P是BC上的点
BP
=2
PC
，
AP
=λ
AB
+μ
AC
，则（　　）
A、λ=2，μ=1
B、λ=1，μ=2
C、λ=
1
3
，μ=
2
3
D、λ=
2
3
，μ=
1
3
分析：如图所示，由
BP
=2
PC
，可得
BP
=
2
3
BC
；利用向量的运算法则可得
BC
=
AC
-
AB
，因此
BP
=
2
3
(
AC
-
AB)
．故
AP
=
AB
+
BP
=
AB
+
2
3
(
AC
-
AB
)=
1
3
AB
+
2
3
AC
．又由
AP
=λ
AB
+μ
AC
．根据向量相等即可得出．
解答：解：如图所示，精英家教网
∵
BP
=2
PC
，∴
BP
=
2
3
BC
，
∵
BC
=
AC
-
AB
，∴
BP
=
2
3
(
AC
-
AB)
．
∴
AP
=
AB
+
BP
=
AB
+
2
3
(
AC
-
AB
)=
1
3
AB
+
2
3
AC
．
又
AP
=λ
AB
+μ
AC
．
∴λ=
1
3
，μ=
2
3
．
故选C．
点评：熟练掌握向量的共线定理及运算法则、向量相等是解题的关键．
练习册系列答案
相关题目
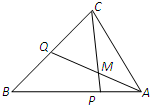如图，在△ABC中，点P是AB上的一点，且
CP 
=
2
3
CA 
+
1
3
CB 
，Q是BC的中点，AQ与CP交于点M，设
CM 
=λ 
CP 
，
AM 
=μ 
AQ 
则实数λ+μ=（　　）
（2011•重庆一模）在△ABC中，点P是AB上一点，且
CP
=
2
3
CA
+
1
3
CB
，又
AP
=t
AB
，则t的值为（　　）
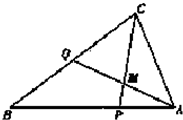（2010•武汉模拟）在△ABC中，点P是AB上一点，且
CP
=
2
3
CA
+
1
3
CB
，Q是BC中点，AQ与CP交点为M，又
CM
=t
CP
，则t=（　　）
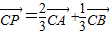如图，在△ABC中，点P是AB上的一点，且，Q是BC的中点，AQ与CP交于点M，设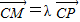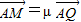，则实数λ+μ=（ ）

A．
B．
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网