Question

已知△ABC中，三个内角A、B、C对应的三边长分别为a、b、c，且有4bcosAcosB=9asin²B。
（Ⅰ）求tanAtanB的值；
（Ⅱ）求tanC的最大值，并判断此时△ABC的形状。

Answer 1

解：（Ⅰ）∵4bcosAcosB=9asin²B
∴4cosAcosB=9sinAsinB
显然cosAcosB≠0
∴tanAtanB=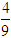
（Ⅱ）由（Ⅰ）知tanAtanB=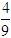>0，故有tanA>0，tanB>0
∴tanA+tanB≥2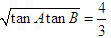
∴tanC=tan[π-（A+B）]=-tan（A+B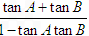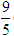）= -= -（tanA+tanB）
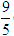            ≤-×2=-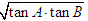
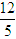
当且仅当tanA=tanB，即A=B时，tanC取得最大值-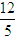，此时△ABC为等腰三角形。