题目内容
(2013•淄博二模)已知△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2-c2,则tanC等于( )
分析:首先由三角形面积公式得到S△ABC=
ab•sinC,再由余弦定理,结合2S=(a+b)2-c2,得出sinC-2cosC=2,然后通过(sinC-2cosC)2=4,求出结果即可.
| 1 |
| 2 |
解答:解:△ABC中,∵S△ABC=
ab•sinC,由余弦定理:c2=a2+b2-2abcosC,
且 2S=(a+b)2-c2 ,∴absinC=(a+b)2-(a2+b2-2abcosC),
整理得sinC-2cosC=2,∴(sinC-2cosC)2=4.
∴
=4,化简可得 3tan2C+4tanC=0.
∵C∈(0,180°),∴tanC=-
,
故选C.
| 1 |
| 2 |
且 2S=(a+b)2-c2 ,∴absinC=(a+b)2-(a2+b2-2abcosC),
整理得sinC-2cosC=2,∴(sinC-2cosC)2=4.
∴
| (sinC-2cosC)2 |
| sin2C+cos2C |
∵C∈(0,180°),∴tanC=-
| 4 |
| 3 |
故选C.
点评:本题考查了余弦定理、三角形面积公式以及三角函数的化简求值,要注意角C的范围,属于中档题.

练习册系列答案
相关题目
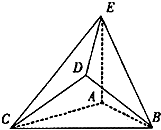 (2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
(2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD. (2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=
(2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=