题目内容
8.已知函数f(x)=e-x-|lnx|的两个零点分别为x1,x2,则( )| A. | 0<x1x2<1 | B. | x1x2=1 | C. | 1<x1x2<e | D. | x1x2>e |
分析 利用函数的零点,判断零点的范围,利用指数函数的单调性以及对数运算法则,推出结果即可.
解答 解:函数f(x)=e-x-|lnx|的两个零点分别为x1,x2,
不妨设0<x1<1<x2,则${e}^{{-x}_{1}}>{e}^{-{x}_{2}}$,${e}^{{-x}_{1}}=-ln{x}_{1}$,${e}^{-{x}_{2}}=ln{x}_{2}$,
所以-lnx1>lnx2,ln(x1x2)<0,0<x1x2<1.
故选:A.
点评 本题考查函数的零点判定定理以及函数的性质的应用,考查计算能力.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
18.若1≤log2(x-y+1)≤2,|x-3|≤1,则x-2y的最大值与最小值之和是( )
| A. | 0 | B. | -2 | C. | 2 | D. | 6 |
3.已知$f(x)=\frac{lnx}{x}$,则( )
| A. | f(2)>f(e)>f(3) | B. | f(3)>f(e)>f(2) | C. | f(3)>f(2)>f(e) | D. | f(e)>f(3)>f(2) |
20.要测量电视塔AB的高度,在C点测得塔顶的仰角是45°,在D点测得塔顶的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度是( )
| A. | 30m | B. | 40m | C. | $40\sqrt{3}$m | D. | $40\sqrt{2}$m |
18.已知全集U={1,2,3,4,5,6,7},集合A={1,3,7},B={x|x=log2(a+1),a∈A},则(∁UA)∩(
(∁UB)=( )
(∁UB)=( )
| A. | {1,3} | B. | {5,6} | C. | {4,5,6} | D. | {4,5,6,7} |
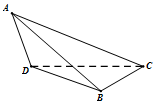 如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形.
如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形. 已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.
已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$. 四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )
四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )