题目内容
9.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第三天走了( )| A. | 60里 | B. | 48里 | C. | 36里 | D. | 24里 |
分析 由题意得:每天行走的路程成等比数列{an}、且公比为$\frac{1}{2}$,由条件和等比数列的前项和公式求出a1,由等比数列的通项公式求出答案即可.
解答 解:由题意得,每天行走的路程成等比数列{an},且公比为$\frac{1}{2}$,
∵6天后共走了378里,∴S6=$\frac{{a}_{1}(1-\frac{1}{{2}^{6}})}{1-\frac{1}{2}}=378$,
解得a1=192,
∴第三天走了a3=a1×$(\frac{1}{2})^{2}$=192×$\frac{1}{4}$=48,
故选B.
点评 本题考查等比数列的前项和公式、通项公式的实际应用,属于基础题.

练习册系列答案
相关题目
20.要测量电视塔AB的高度,在C点测得塔顶的仰角是45°,在D点测得塔顶的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度是( )
| A. | 30m | B. | 40m | C. | $40\sqrt{3}$m | D. | $40\sqrt{2}$m |
18.已知全集U={1,2,3,4,5,6,7},集合A={1,3,7},B={x|x=log2(a+1),a∈A},则(∁UA)∩(
(∁UB)=( )
(∁UB)=( )
| A. | {1,3} | B. | {5,6} | C. | {4,5,6} | D. | {4,5,6,7} |
19.已知函数f(x)=ln$\frac{x}{2}$+$\frac{1}{2}$,g(x)=ex-2,对?m∈R,?n∈(0,+∞)使得g(m)=f (n)成立,则n-m的最小值为( )
| A. | -ln 2 | B. | ln 2 | C. | 2$\sqrt{e}$-3 | D. | e2-3 |
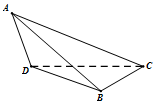 如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形.
如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形. 四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )
四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )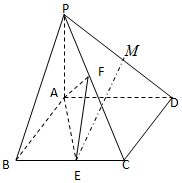 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,E是BC中点,M是PD上的中点,F是PC上的动点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,E是BC中点,M是PD上的中点,F是PC上的动点.