题目内容
做同时抛掷两颗骰子的试验,如果至少出现一个3点或6点,应当称这次试验是“完美试验”,那么在54次完全相同的试验中“完美试验”的次数X的期望E(X)是 .
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:抛掷两个骰子,出现的点数情况共有36种,至少有一个3点或一个6点出现的情况有20种,在54次完全相同的试验中“完美试验”的次数X~B(54,
),由此能求出EX.
| 5 |
| 9 |
解答:
解:∵抛掷两个骰子,出现的点数情况共有36种,
至少有一个3点或一个6点出现的情况有20种,
∴一次试验中是“完美试验”概率为p=
=
.
∴在54次完全相同的试验中“完美试验”的次数X~B(54,
),
∴EX=54×
=30.
故答案为:30.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
∴一次试验中是“完美试验”概率为p=
| 20 |
| 36 |
| 5 |
| 9 |
∴在54次完全相同的试验中“完美试验”的次数X~B(54,
| 5 |
| 9 |
∴EX=54×
| 5 |
| 9 |
故答案为:30.
点评:本题考查离散型随机变量的数学期望的求法,是中档题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
已知数列{an}为等差数列,且a3=9,a5=3,则a9等于( )
| A、-9 | B、-6 | C、-3 | D、27 |
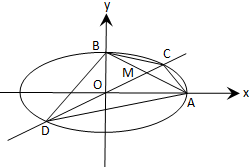 如图所示,已知A,B分别是椭圆E:
如图所示,已知A,B分别是椭圆E:
