题目内容
10.设f(n)=($\frac{1+i}{1-i}$)n+($\frac{1-i}{1+i}$)n(n∈N*),则集合{f(n)}中元素的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 无数个 |
分析 化简复数$\frac{1+i}{1-i}$与$\frac{1-i}{1+i}$,再根据i的性质,计算f(n)的值.
解答 解:化简复数$\frac{1+i}{1-i}$=$\frac{(1+i)(1+i)}{(1-i)(1+i)}$=i,
$\frac{1-i}{1+i}$=$\frac{(1-i)(1-i)}{(1+i)(1-i)}$=-i,
∴f(n)=($\frac{1+i}{1-i}$)n+($\frac{1-i}{1+i}$)n
=in+(-i)n,
根据i的性质,对指数是1,2,3,4四个数字进行检验即可,
∵f(1)=0,f(2)=-2,
f(3)=0,f(4)=2;
∴集合{f(n)}中共有3个元素.
故选:C.
点评 本题考查了复数的化简与运算问题,也考查了虚数单位的性质与应用问题,是基础题目.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
15.若变量x,y满足$\left\{\begin{array}{l}{2x+y-5≥0}\\{x-y+5≥0}\\{2x-y-5≤0}\end{array}\right.$ 则x2+y2的最小值为( )
| A. | $\frac{25}{4}$ | B. | $\frac{5}{2}$ | C. | $\sqrt{5}$ | D. | 5 |
11.若双曲线M:$\frac{{x}^{2}}{m}$-$\frac{{y}^{2}}{6}$=1(m>0)的离心率为2,则双曲线N:x2-$\frac{{y}^{2}}{m}$=1的渐近线方程为( )
| A. | y=±$\sqrt{2}$x | B. | y=±2x | C. | y=±$\sqrt{3}$x | D. | y=±2$\sqrt{2}$x |
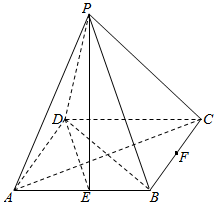 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.