题目内容
1.在等比数列{an}中,a1=1,an=256,q=2,则n=9.分析 利用等比数列的通项公式即可得出.
解答 解:由已知可得:256=1×2n-1,
解得n=9.
故答案为:9.
点评 本题考查了等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
12.数列a1,a2,…,a7,其中恰好有5个2和2个4,调换a1至a7各数的位置,一共可以组成不同的数列(含原数列( )
| A. | 21个 | B. | 25个 | C. | 32个 | D. | 42个 |
13.已知a>0,b>0,则$\frac{a+b}{2}$,$\sqrt{ab}$,$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$,$\frac{2ab}{a+b}$中最小的是( )
| A. | $\frac{a+b}{2}$ | B. | $\sqrt{ab}$ | C. | $\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$ | D. | $\frac{2ab}{a+b}$ |
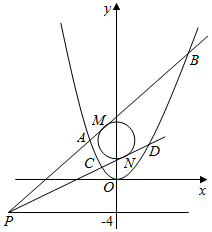 在直角坐标系xOy中,抛物线C1:x2=4y和圆C2:x2+(y-5)2=9,点P是直线y=-4上的动点.
在直角坐标系xOy中,抛物线C1:x2=4y和圆C2:x2+(y-5)2=9,点P是直线y=-4上的动点.