题目内容
10．已知数列{an}的前n项和为Sn，数列{bn}，{cn}满足 （n+1）bn=an+1-$\frac{Sn}{n}$，（n+2）cn=$\frac{{a}_{n+1}+{a}_{n+2}}{2}$-$\frac{{S}_{n}}{n}$，其中n∈N*．（1）若数列{an}是公差为2的等差数列，求数列{cn}的通项公式；
（2）若存在实数λ，使得对一切n∈N*，有bn≤λ≤cn，求证：数列{an}是等差数列．
分析 （1）数列{an}是公差为2的等差数列，可得an=a1+2（n-1），$\frac{{S}_{n}}{n}$=a1+n-1．代入（n+2）cn=$\frac{{a}_{n+1}+{a}_{n+2}}{2}$-$\frac{{S}_{n}}{n}$即可得出cn．
（2）由（n+1）bn=an+1-$\frac{Sn}{n}$，可得：n（n+1）bn=nan+1-Sn，（n+1）（n+2）bn+1=（n+1）an+2-Sn+1，相减可得：an+2-an+1=（n+2）bn+1-nbn，代入化简可得cn=$\frac{1}{2}$（bn+bn-1）．bn≤λ≤cn，λ≤cn=$\frac{1}{2}$（bn+bn-1）≤λ，故bn=λ，cn=λ．进而得出．
解答 （1）解：∵数列{an}是公差为2的等差数列，∴an=a1+2（n-1），$\frac{{S}_{n}}{n}$=a1+n-1．
∴（n+2）cn=$\frac{{a}_{1}+2n+{a}_{1}+2（n+1）}{2}$-（a1+n-1）=n+2，解得cn=1．
（2）证明：由（n+1）bn=an+1-$\frac{Sn}{n}$，
可得：n（n+1）bn=nan+1-Sn，（n+1）（n+2）bn+1=（n+1）an+2-Sn+1，
相减可得：an+2-an+1=（n+2）bn+1-nbn，
可得：（n+2）cn=$\frac{{a}_{n+1}+{a}_{n+2}}{2}$-$\frac{{S}_{n}}{n}$=$\frac{{a}_{n+1}+{a}_{n+2}}{2}$-[an+1-（n+1）bn]
=$\frac{{a}_{n+2}-{a}_{n+1}}{2}$+（n+1）bn=$\frac{（n+2）{b}_{n+1}-n{b}_{n}}{2}$+（n+1）bn=$\frac{n+2}{2}$（bn+bn-1），
因此cn=$\frac{1}{2}$（bn+bn-1）．∵bn≤λ≤cn，
∴λ≤cn=$\frac{1}{2}$（bn+bn-1）≤λ，故bn=λ，cn=λ．
∴（n+1）λ=an+1-$\frac{{S}_{n}}{n}$，（n+2）λ=$\frac{1}{2}$（an+1+an+2）-$\frac{{S}_{n}}{n}$，
相减可得：$\frac{1}{2}$（an+2-an+1）=λ，即an+2-an+1=2λ，（n≥2）．
又2λ=${a}_{2}-\frac{{S}_{1}}{1}$=a2-a1，则an+1-an=2λ（n≥1），∴数列{an}是等差数列．
点评 本题考查了数列递推关系、等差数列的定义通项公式、不等式的性质，考查了推理能力与计算能力，属于难题．
名校课堂系列答案
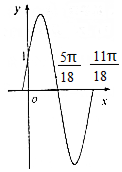函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象如图所示，则f（$\frac{5π}{9}$）的值是（ ）| A． | 1 | B． | -1 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{5π}{12}$ |