题目内容
15.函数f(x)=2sin(2x-$\frac{π}{3}$)的图象关于直线x=x0对称,则|x0|的最小值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{5π}{12}$ |
分析 利用正弦函数的对称轴方程即可求解.
解答 解:函数f(x)=2sin(2x-$\frac{π}{3}$),
其对称轴方程:2x-$\frac{π}{3}$=-$\frac{π}{2}+kπ$,
可得:x=$\frac{1}{2}kπ-\frac{π}{12}$,(k∈Z)
则x0=$\frac{1}{2}kπ-\frac{π}{12}$,
即为|$\frac{1}{2}kπ-\frac{π}{12}$|的最小值.
当k=0时,|x0|的最小值为$\frac{π}{12}$
故选:A.
点评 本题主要考查三角函数的图象和性质的运用,对称轴方程的求法.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知全集U={x∈N|x≤5},若A={x∈N|2x-5<0},则∁UA=( )
| A. | {3,4} | B. | {3,4,5} | C. | {2,3,4,5} | D. | {4,5} |
4.已知函数f(x)=Asin(ωx+φ)(A≠0,ω>0,0<φ<$\frac{π}{2}$),若f($\frac{2π}{3}$)=-f(0),则ω的最小值为( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
3.某人抛掷一枚质地均匀的硬币100次,结果出现了50次正面向上.如果他将这枚硬币抛掷1000次,那么出现正面向上的次数,在下面四个选项中,最合适的选项是( )
| A. | 恰为500次 | B. | 恰为600次 | C. | 500次左右 | D. | 600次左右 |
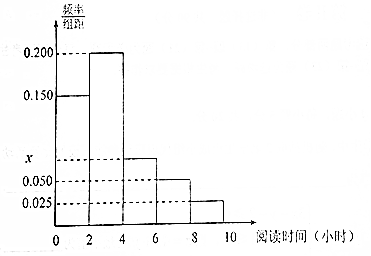 某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:
某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图: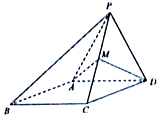 如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.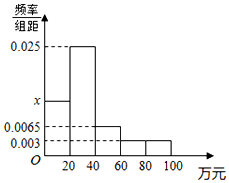 某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为第一组[0,20),第二组AA1⊥平面ABC,第三组[40,60),第四组[60,80),第五组[80,100].
某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为第一组[0,20),第二组AA1⊥平面ABC,第三组[40,60),第四组[60,80),第五组[80,100].