题目内容
18.在矩形ABCD中,AB=4,BC=2,E为BC的中点,若F为该矩形内(含边界)任意一点,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的最大值为18.分析 可分别以直线DC,DA为x轴,y轴,建立平面直角坐标系,进而求出A,E的坐标,并设F(x,y),从而可求出$\overrightarrow{AE}•\overrightarrow{AF}=4x-y+2$,这样设z=4x-y+2,利用线性规划的方法即可求出z的最大值,即求出数量积的最大值.
解答 解:据条件,分别以边DC,DA所在直线为x,y轴,建立如图所示平面直角坐标系,则: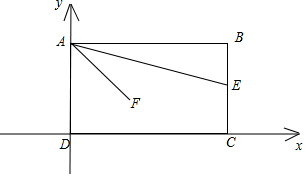
A(0,2),E(4,1),设F(x,y),x0≤x≤4,0≤y≤2;
∴$\overrightarrow{AE}=(4,-1),\overrightarrow{AF}=(x,y-2)$;
∴$\overrightarrow{AE}•\overrightarrow{AF}=4x-y+2$;
设z=4x-y+2,则y=4x+(2-z);
∴2-z是直线y=4x+(2-z)在y轴上的截距,截距最小时,z最大;
可看出直线y=4x+(2-z)过点C(4,0)时z最大;
即0=16+2-z,z=18.
故答案为:18.
点评 考查通过建立坐标系,利用坐标解决向量问题的方法,能确定平面上点的坐标,数量积的坐标运算,线性规划求最值的方法.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
11.在△ABC中,AC=$\sqrt{13}$,BC=1,B=60°,则△ABC的面积为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3 |
3.某人抛掷一枚质地均匀的硬币100次,结果出现了50次正面向上.如果他将这枚硬币抛掷1000次,那么出现正面向上的次数,在下面四个选项中,最合适的选项是( )
| A. | 恰为500次 | B. | 恰为600次 | C. | 500次左右 | D. | 600次左右 |
7.命题p:关于x的方程x2+ax+2=0无实根,命题q:函数f(x)=logax在(0,+∞)上单调递增,若“p∧q”为假命题,“p∨q”真命题,则实数a的取值范围是( )
| A. | (-2$\sqrt{2}$,+∞) | B. | (-2$\sqrt{2}$,2$\sqrt{2}$) | C. | (-2$\sqrt{2}$,1]∪[2$\sqrt{2}$,+∞) | D. | (-∞,2$\sqrt{2}$) |
 如图是某赛季甲、乙两名篮球运动员每场比赛得分情况的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是35,26.
如图是某赛季甲、乙两名篮球运动员每场比赛得分情况的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是35,26.