题目内容
18．若复数z满足z（1-i）=2i（i是虚数单位），$\overline{z}$是z的共轭复数，则$\overline{z}$=-1-i．分析 把已知等式变形，再由复数代数形式的乘除运算化简求得z，进一步求得$\overline{z}$．
解答 解：∵z（1-i）=2i，
∴$z=\frac{2i}{1-i}=\frac{2i（1+i）}{（1-i）（1+i）}=\frac{-2+2i}{2}=-1+i$，
∴$\overline{z}=-1-i$．
故答案为：-1-i．
点评 本题考查复数代数形式的乘除运算，考查了共轭复数的概念，是基础题．
练习册系列答案
相关题目
6．已知全集U={x∈N|x≤5}，若A={x∈N|2x-5＜0}，则∁UA=（ ）
| A． | {3，4} | B． | {3，4，5} | C． | {2，3，4，5} | D． | {4，5} |
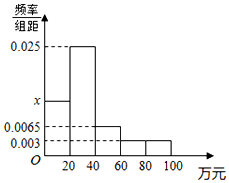某市随机抽取部分企业调查年上缴税收情况（单位：万元），将所得数据绘制成频率分布直方图（如图），年上缴税收范围是[0，100]，样本数据分组为第一组[0，20），第二组AA1⊥平面ABC，第三组[40，60），第四组[60，80），第五组[80，100]．