题目内容
14．若x，y满足条件$\left\{\begin{array}{l}{2x-y≤1}\\{x+y≥2}\\{y-x≤2}\end{array}\right.$，目标函数z=-3x+2y的最小值为-1．分析 作出可行域，变形目标函数，平移直线y=$\frac{3}{2}$x+$\frac{1}{2}$z结合图象可得．
解答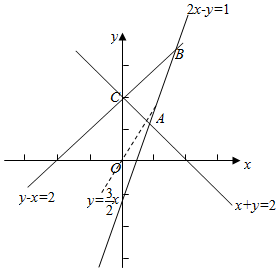 
解：作出x，y满足条件$\left\{\begin{array}{l}{2x-y≤1}\\{x+y≥2}\\{y-x≤2}\end{array}\right.$，所对应的可行域（如图△ABC），
变形目标函数可得y=$\frac{3}{2}$x+$\frac{1}{2}$z，平移直线y=$\frac{3}{2}$x+$\frac{1}{2}$z可知：
当直线经过点A时，直线的截距最小，
解方程组$\left\{\begin{array}{l}{x+y=2}\\{2x-y=1}\end{array}\right.$可解得A（1，1）
此时目标函数z取最小值z=-3+2=-1，
故答案为：-1．
点评 本题考查简单线性规划，准确作图是解决问题的关键，属中档题．
练习册系列答案
相关题目
4．一个体积为12$\sqrt{3}$的正棱柱的三视图，如图所示，则该三棱柱的高为（ ）
| A． | 3 | B． | $3\sqrt{3}$ | C． | $2\sqrt{3}$ | D． | 4 |
5．数学与文学有许多奇妙的联系，如诗中有回文诗：“儿忆父兮妻忆夫”，既可以顺读也可以逆读，数学中有回文数，如343、12521等，两位数的回文数有11、22、33、…、99共9个，则三位数的回文数中为偶数的概率是（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{2}{9}$ | C． | $\frac{3}{9}$ | D． | $\frac{4}{9}$ |
19．某种产品在五个年度的广告费用支出x万元与销售额y万元的统计数据如下表：
（I）根据上表提供的数据，求出y关于x的线性回归方程；
（II）据此模型估计某年度产品的销售额欲达到108万元，那么本年度收入的广告费约为多少万元？（回归方程为y=${\;}_{b}^{∧}$x+${\;}_{a}^{∧}$其中：${\;}_{b}^{∧}$=$\frac{{\sum_{i=1}^{n}{x}_{i}y}_{i}-{{n}_{x}^{-}}_{y}^{-}}{\sum_{i=1}^{n}{x}_{i}^{2}-{{n}_{x}^{-}}^{2}}$，${\;}_{a}^{∧}$=${\;}_{y}^{∧}$-${\;}_{b}^{∧}$${\;}_{x}^{-}$）
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 35 | 50 | 55 | 80 |
（II）据此模型估计某年度产品的销售额欲达到108万元，那么本年度收入的广告费约为多少万元？（回归方程为y=${\;}_{b}^{∧}$x+${\;}_{a}^{∧}$其中：${\;}_{b}^{∧}$=$\frac{{\sum_{i=1}^{n}{x}_{i}y}_{i}-{{n}_{x}^{-}}_{y}^{-}}{\sum_{i=1}^{n}{x}_{i}^{2}-{{n}_{x}^{-}}^{2}}$，${\;}_{a}^{∧}$=${\;}_{y}^{∧}$-${\;}_{b}^{∧}$${\;}_{x}^{-}$）
3．下列命题中为真命题的是（ ）
| A． | 命题“若x＞y则x＞|y|”的逆命题 | |
| B． | 命题“若x=1，则x2+x-2=0”的否命题 | |
| C． | 命题“若x＞1，则x2＞1”的否命题 | |
| D． | 命题“若x2＞0，则函数x＞1”的逆否命题 |
3．记Sn为等差数列{an}的前n项和，若a3+a4=8，S8=48，则{an}的公差为（ ）
| A． | 1 | B． | 2 | C． | 4 | D． | 8 |