题目内容
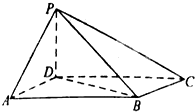如图，在四棱锥P-ABCED中，PD⊥面ABCD，四边形ABCD为平行四边形，∠DAB=60°，AB=PA=2AD=4，（1）若E为PC中点，求证：PA∥平面BDE
（2）求三棱锥D-BCP的体积．
考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）连结AC，BD，交于点O，连结OE，则OE∥AP，由此能证明PA∥平面BDE．
（2）求出S△BDC=
×4×2×sin60°=2
，PD=
=2
，由VD-BCP=VP-DBC=
S△DBC•PD，能求出三棱锥D-BCP的体积．
（2）求出S△BDC=
| 1 |
| 2 |
| 3 |
| 16-4 |
| 3 |
| 1 |
| 3 |
解答：
（1）证明：连结AC，BD，交于点O，
∵四边形ABCD为平行四边形，∴O是AC中点，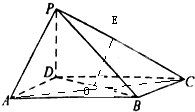
∵E是PC中点，∴OE∥AP，
又AP?平面BDE，OE?平面BDE，
∴PA∥平面BDE．
（2）解：∵S△BDC=
×4×2×sin60°=2
，
PD=
=2
，
∴VD-BCP=VP-DBC=
S△DBC•PD=
×2
×2
=4．
∵四边形ABCD为平行四边形，∴O是AC中点，
∵E是PC中点，∴OE∥AP，
又AP?平面BDE，OE?平面BDE，
∴PA∥平面BDE．
（2）解：∵S△BDC=
| 1 |
| 2 |
| 3 |
PD=
| 16-4 |
| 3 |
∴VD-BCP=VP-DBC=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
点评：本题考查直线与平面平行的证明，考查三棱锥的体积的求法，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
在长为16cm的线段AB上任取一点M，并以线段AM为一边作正方形，则此正方形的面积介于25cm2与81cm2之间的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，∠BAC=45°，AC=a，AB=
AC，E，F为边BC的三等分点，则
•
=（ ）
| 2 |
| AE |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=（
）
的值域为（ ）
| 1 |
| 3 |
| x-1 |
| A、（-∞，0） | B、（0，1] |
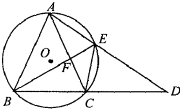如图，⊙O是等腰三角形ABC的外接圆，AB=AC，延长BC到点D，使CD=AC，连接AD交⊙O于点E，连接BE与AC交于点F．