题目内容
已知直线l的参数方程是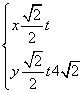 (t是参数),圆C的极坐标方程为ρ=2cosθ+
(t是参数),圆C的极坐标方程为ρ=2cosθ+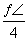 .
.
(1)求圆心C的直角坐标;
(2)由直线l上的点向圆C引切线,求切线长的最小值.
解:(1)∵ρ= cos θ-
cos θ- sin θ,∴ρ2=
sin θ,∴ρ2= ρcos θ-
ρcos θ- ρsin θ,
ρsin θ,
∴圆C的直角坐标方程为x2+y2- x+
x+ y=0.即
y=0.即 =1,
=1,
l ∴圆心C的直角坐标为
(2)直线l上的点向圆C引切线,切线长是
 ≥2
≥2  .
.
∴直线l上的点向圆C引的切线的切线长的最小值是2  .
.

练习册系列答案
相关题目

 (B)
(B) (C)
(C) (D)
(D)
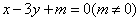 与双曲线
与双曲线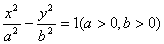 的两条渐近线分别交于点
的两条渐近线分别交于点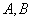 ,若点
,若点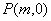 满足
满足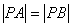 ,则该双曲线的离心率是________.
,则该双曲线的离心率是________. 关于运算
关于运算 满足:(1)对任意的
满足:(1)对任意的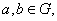 都有
都有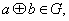 (2)存在
(2)存在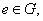 都有
都有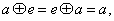 (3) 对任意的
(3) 对任意的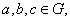 都有
都有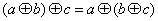 ,则称
,则称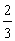 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.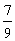 ,求
,求 ;
; 上的一点
上的一点 到焦点的距离为1,则点
到焦点的距离为1,则点 B.
B. C.
C. D.
D.
 的倾斜角的余弦值为________.
的倾斜角的余弦值为________.
