题目内容
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为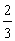 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(Ⅰ)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为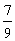 ,求
,求 ;
;
(Ⅱ)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
【解析】(Ⅰ)由已知得,张三中奖的概率为 ,李四中奖的概率为
,李四中奖的概率为 ,且两人中奖与否互不影响.
,且两人中奖与否互不影响.
记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件为“X=5”,
因为P(X=5)= ×
× ,所以P (A)=1-P(X=5)=1-
,所以P (A)=1-P(X=5)=1- ×
× =
=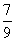 ,所以
,所以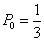 .……6分
.……6分
(Ⅱ)设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,
则这两人选择方案甲抽奖累计得分的数学期望为E(2X1),
选择方案乙抽奖累计得分的数学期望为E(3X2).
由已知可得,X1~B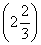 ,X2~B
,X2~B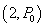 ,
,
所以E(X1)=2× =
=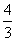 ,E(X2)=2×
,E(X2)=2× ,
,
从而E(2X1)=2E(X1)= ,E(3X2)=3E(X2)=6
,E(3X2)=3E(X2)=6 .
.
若E(2X1) 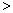 E(3X2),则
E(3X2),则
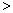 6
6
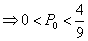 ;
;
若E(2X1) 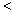 E(3X2),则
E(3X2),则
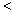 6
6
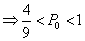 ;
;
若E(2X1) 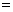 E(3X2),则
E(3X2),则 =6
=6
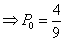 ;
;
综上所述,当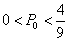 时,他们都选择方案甲进行抽奖,累计得分的数学期望较大;当
时,他们都选择方案甲进行抽奖,累计得分的数学期望较大;当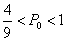 时,他们都选择方案乙进行抽奖,累计得分的数学期望较大;当
时,他们都选择方案乙进行抽奖,累计得分的数学期望较大;当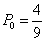 时,他们选择方案甲或方案乙进行抽奖,累计得分的数学期望相等…………13分
时,他们选择方案甲或方案乙进行抽奖,累计得分的数学期望相等…………13分

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 ,“函数
,“函数 有零点”是“函数
有零点”是“函数 在
在 上为减函数”的( )
上为减函数”的( ) .
.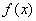 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数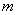 的取值范围;
的取值范围;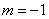 ,试比较当
,试比较当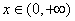 时,
时,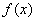 与
与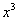 的大小;
的大小;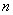 ,不等式
,不等式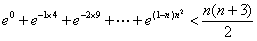 成立.
成立.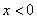 ”是“
”是“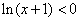 ”的充要条件
”的充要条件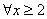 ,
,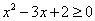 ”的否定是“
”的否定是“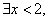
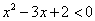 ”
”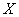 服从正态分布
服从正态分布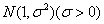 ,若
,若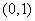 内取值的概率为0.4,则
内取值的概率为0.4,则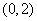 内取值的概率为0.8
内取值的概率为0.8 满足条件:
满足条件: ,则
,则 的最大值是 。
的最大值是 。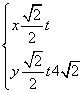 (t是参数),圆C的极坐标方程为ρ=2cosθ+
(t是参数),圆C的极坐标方程为ρ=2cosθ+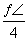 .
. 、
、 、
、 是三个不同的平面,给出下列命题,正确的是( ).
是三个不同的平面,给出下列命题,正确的是( ). ,
, ,则
,则 B.若
B.若 ,
, ,则
,则 ,则
,则 D.若
D.若 ,
, ,
, ,则
,则
 是纯虚数,则实数等于
是纯虚数,则实数等于 C.
C. D.
D.
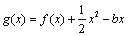 ,函数
,函数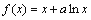 在x=1处的切线与直线
在x=1处的切线与直线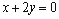 垂直.
垂直.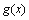 存在单调递减区间,求实数
存在单调递减区间,求实数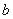 的取值范围;
的取值范围;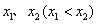 是函数
是函数 ,求
,求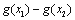 的最小值.
的最小值.