Question

将边长为2，锐角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD，点E、F分别为AC、BD的中点，给出下列三个命题：
①EF∥AB；
②EF是异面直线AC与BD的公垂线；
③AC垂直于截面BDE．
其中正确命题的序号是

 

．（写出所有正确命题的序号）

Answer 1

考点：命题的真假判断与应用

专题：空间位置关系与距离

分析：①作出图形，可知EF与AB异面，可判断①；
②利用等腰三角形底边中线的性质易证BE⊥AC，DE⊥AC，EF⊥BD；再利用线面垂直的判定定理可证AC垂直于截面BDE，从而可判断②
③由②知，AC⊥平面BDE，可判断③．

解答： 解：将边长为2，锐角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD，如图，

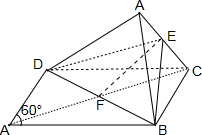
对于①，由图可知，EF与AB异面，故①错误；
对于②，∵点E、F分别为AC、BD的中点，AB=BC，DC=DA，
∴BE⊥AC，DE⊥AC，BE∩DE=E，
∴AC⊥平面BDE，EF?平面BDE，
∴AC⊥EF；
又BE=DE，F为BD的中点，
∴EF⊥BD；
∴EF是异面直线AC与BD的公垂线，故②正确；
对于③，由②知，AC⊥平面BDE，故③正确；
综上所述，正确命题的序号是②③．
故答案为：②③．

点评：本题考查空间直线与直线之间的位置关系，考查线面垂直的判定，作图是关键，考查推理、证明的能力，属于中档题．