题目内容
19.已知点P时抛物线y2=-4x上的动点,设点P到此抛物线的准线的距离为d1,到直线x+y-4=0的距离为d2,则d1+d2的最小值是( )| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{5\sqrt{2}}{2}$ |
分析 点P到准线的距离等于点P到焦点F的距离,过焦点F作直线x+y-4=0的垂线,此时d1+d2最小,根据抛物线方程求得F,进而利用点到直线的距离公式求得d1+d2的最小值.
解答 解:点P到准线的距离等于点P到焦点F的距离,
过焦点F作直线x+y-4=0的垂线,此时d1+d2最小,
∵F(-1,0),则d1+d2=$\frac{|-1+0-4|}{\sqrt{2}}$=$\frac{5\sqrt{2}}{2}$.
故选:D.
点评 本题主要考查了抛物线的简单性质,两点距离公式的应用,直线与抛物线的简单性质的应用,是中档题.

练习册系列答案
相关题目
9.已知$\overrightarrow{OA}$=(cos2x,-1),$\overrightarrow{OB}$=(1,sin2x+$\sqrt{3}$sin2x)(x∈R),若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OB}$,则函数f(x)的最小正周期( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
14.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),则下列向量中与向量2$\overrightarrow{a}$+$\overrightarrow{b}$垂直的是( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\overrightarrow{a}$-$\overrightarrow{b}$ | C. | 2$\overrightarrow{a}$-$\overrightarrow{b}$ | D. | $\overrightarrow{a}$-2$\overrightarrow{b}$ |
11.执行如图所示的程序框图,则输出的结果是( )

| A. | 8 | B. | 13 | C. | 21 | D. | 34 |
 某次数学测验,12名同学分数的茎叶图如图:则这些分数的中位数是80.
某次数学测验,12名同学分数的茎叶图如图:则这些分数的中位数是80.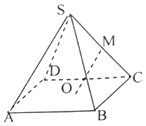 如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$.
如图,已知正四棱锥侧S-ABCD棱长为2,底面边长为$\sqrt{2}$,点O为底面ABCD中心,点M为SC中点,则异面直线OM与SB所成角的余弦值为$\frac{3}{4}$. 如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).