题目内容
长方形OABC各点的坐标如图所示,D为OA的中点,由D点发出的一束光线,入射到边AB上的点E处,经AB、BC、CO一次反射后恰好经过点A,则入射光线DE所在的直线斜率为 .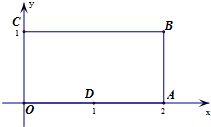

考点:与直线关于点、直线对称的直线方程
专题:直线与圆
分析:设入射光线DE的倾斜角为θ,则由题意可得反射线GA的倾斜角为π-θ.用点斜式求得GA的方程,可得点G的坐标;再用点斜式求得FE的方程,可得点E的坐标.直角三角形DAE中,利用直角三角形中的边角关系求得tanθ 的值,可得DE的斜率.
解答:
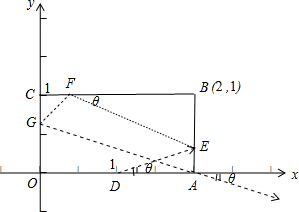 解:如图所示:设入射光线DE的倾斜角为θ,则由题意可得反射线GA的倾斜角为π-θ,
解:如图所示:设入射光线DE的倾斜角为θ,则由题意可得反射线GA的倾斜角为π-θ,
故GA的斜率为tan(π-θ)=-tanθ,故GA的方程为y-0=-tanθ(x-2),
故点G的坐标为(0,2tanθ).
直线FE的斜率为tan(π-θ)=-tanθ,CG=1-OG=1-2tanθ,CF=
=
-2),
点F的坐标为(
-2,1),故FE的方程为y-1=-tanθ(x-
+2),
故点E(2,2-4tanθ).
直角三角形DAE中,由tan∠ADE=tanθ=
=AE=2-4tanθ,
求得tanθ=
,故DE的斜率为
,
故答案为:
.
 解:如图所示:设入射光线DE的倾斜角为θ,则由题意可得反射线GA的倾斜角为π-θ,
解:如图所示:设入射光线DE的倾斜角为θ,则由题意可得反射线GA的倾斜角为π-θ,故GA的斜率为tan(π-θ)=-tanθ,故GA的方程为y-0=-tanθ(x-2),
故点G的坐标为(0,2tanθ).
直线FE的斜率为tan(π-θ)=-tanθ,CG=1-OG=1-2tanθ,CF=
| CG |
| tanθ |
| 1 |
| tanθ |
点F的坐标为(
| 1 |
| tanθ |
| 1 |
| tanθ |
故点E(2,2-4tanθ).
直角三角形DAE中,由tan∠ADE=tanθ=
| AE |
| AD |
求得tanθ=
| 2 |
| 5 |
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:本题主要考查反射定理的应用,用点斜式求直线的方程,直角三角形中的边角关系,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合A={1,2,3,4,5},B={y|y=2x,x∈A},则A∩B=( )
| A、{1,2,3,4,5} |
| B、{1,2,3,4,5,6,8,10} |
| C、{2,4} |
| D、∅ |
已知双曲线
-y2=1(a>0)的左焦点与抛物线y2=-12x的焦点重合,则此双曲线的渐近线方程是( )
| x2 |
| a2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±2
| ||||
D、y=±
|
若函数f(x),g(x)分别是定义在R上的奇函数,则有( )
| A、f(0)=g(0) |
| B、f(0)>g(0) |
| C、f(0)<g(0) |
| D、无法比较 |
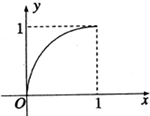 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: