题目内容
14.(x-1)10(x2+x+1)展开式中x2项的系数为36.分析 求出(x-1)10的通项公式,考虑r=8,r=9,R=10时的系数,相加求和即可得到所求值.
解答 解:(x-1)10的通项公式为Tr+1=${C}_{10}^{r}$x10-r(-1)r,r=0,1,2,…,10,
则(x2+x+1)(x-$\frac{1}{x}$)6的展开式中x2项的系数为
(-1)10+(-1)9${C}_{10}^{9}$+(-1)8${C}_{10}^{8}$=1-10+45=36.
故答案为:36.
点评 本题考查了二项式定理的应用,注意运用分类组合法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.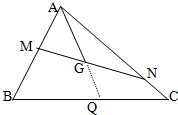 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )
 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
3.已知函数f(x)=Asin($\frac{π}{2}$x-$\frac{π}{2}$),g(x)=k(x-3).已知当A=1时,函数h(x)=f(x)-g(x)所有零点和为9.则当A=2时,函数h(x)=f(x)-g(x)所有零点和为( )
| A. | 15 | B. | 12 | C. | 9 | D. | 与k的取值有关 |
2.已知一个几何体的三视图如图所示,则该几何体的体积为( )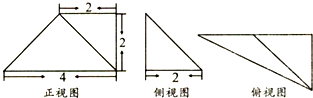

| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
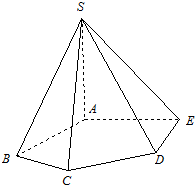 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°