题目内容
3．已知函数f（x）=Asin（$\frac{π}{2}$x-$\frac{π}{2}$），g（x）=k（x-3）．已知当A=1时，函数h（x）=f（x）-g（x）所有零点和为9．则当A=2时，函数h（x）=f（x）-g（x）所有零点和为（ ）| A． | 15 | B． | 12 | C． | 9 | D． | 与k的取值有关 |
分析 函数f（x）与函数g（x）关于点（3，0）对称，h（x）零点关于x=3“对称”，结合函数的图象解答．
解答 解：如图，函数y=f（x）与y=g（x）图象均点过的（3，0），且均关于点（3，0）对称．
∴h（x）零点关于x=3“对称”，∵当A=1时，h（x）所有零点和为9，
∴此时，函数y=f（x）与y=g（x）图象有三个公共点，此时，f（6）＜g（6），得$k＞\frac{1}{3}$．
当A=2时，f（6）＞g（6）且g（9）=6k＞2=fmax（x），
∴h（x）有5个零点x1，x2，3，x4，x5，且x1+x5=x2+x4=6．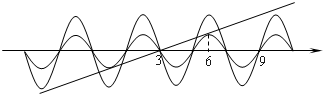
∴x1+x2+3+x4+x5=15，
故选A．
点评 本题主要考查函数的零点，函数的性质，属于基础题．
练习册系列答案
相关题目
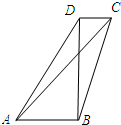如图，在四边形ABCD中，|$\overrightarrow{AB}|+|\overrightarrow{BD|}+|\overrightarrow{DC}$|=4，$（|\overrightarrow{AB}|+|\overrightarrow{DC}|）|\overrightarrow{BD}$|=4，$\overrightarrow{AB}•\overrightarrow{BD}=\overrightarrow{BD}•\overrightarrow{DC}$=0，则$（\overrightarrow{AB}+\overrightarrow{DC}）•\overrightarrow{AC}$的值为（ ）