题目内容
下列函数中,在R内是单调递增函数的是( )
| A、y=2x |
| B、y=log2x |
| C、y=x2 |
| D、y=-x2 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:直接结合常见函数的性质,逐个进行判断即可.
解答:
解:A:y=2x为R上的增函数,符合题意,
B,为(0,+∞)上的增函数,不符合题意,
C,y=x2在(-∞,0)上为减函数,在(0,+∞)上的增函数,不符合题意,
D,y=-x2在(-∞,0)上为增函数,在(0,+∞)上的减函数,不符合题意,
故选A.
B,为(0,+∞)上的增函数,不符合题意,
C,y=x2在(-∞,0)上为减函数,在(0,+∞)上的增函数,不符合题意,
D,y=-x2在(-∞,0)上为增函数,在(0,+∞)上的减函数,不符合题意,
故选A.
点评:本题重点考查函数的单调性,属于基础题.

练习册系列答案
相关题目
执行如图所示的程序框图,如输入x=2,则输出的值为( )


| A、5 |
| B、log85 |
| C、9 |
| D、log89 |
两条直线ax+y+1=0与3x-2y+1=0垂直,则a的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知一个圆锥的侧面展开图为扇形,该扇形的圆心角为
,面积为3π,则此圆锥的体积是( )
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图所示的程序框图,该算法的功能是( )
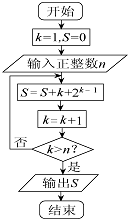

| A、计算(1+20)+(2+21)+(3+22)+…+(n+1+2n)的值 |
| B、计算(1+21)+(2+22)+(3+23)+…+(n+2n)的值 |
| C、计算(1+2+3+…+n)+(20+21+22+…+2n-1)的值 |
| D、计算[1+2+3+…+(n-1)]+(20+21+22+…+2n)的值 |