题目内容
已知函数f(x)=|2x+1|,g(x)=|2x-5|.
(Ⅰ)画出函数y=f(x)-g(x)的图象;
(Ⅱ)解方程:f(x)+g(x)=6.
(Ⅰ)画出函数y=f(x)-g(x)的图象;
(Ⅱ)解方程:f(x)+g(x)=6.
考点:抽象函数及其应用,函数的零点
专题:函数的性质及应用
分析:(Ⅰ)先利用每个绝对值的零点将函数定义域分成几段,然后在每一段上化简其解析式,然后逐段画出其图象;
(Ⅱ)根据(Ⅰ)可知,y=f(x)+g(x)是一个分段函数,因此分段解方程f(x)+g(x)=6.
(Ⅱ)根据(Ⅰ)可知,y=f(x)+g(x)是一个分段函数,因此分段解方程f(x)+g(x)=6.
解答:
解:(I)由已知得y=f(x)-g(x)=
,图象如图所示
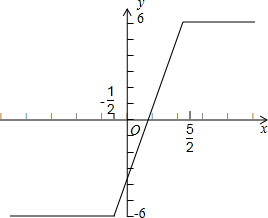
(Ⅱ)由已知得:f(x)+g(x)=|2x+1|+|2x-5|=6,
而f(x)+g(x)=
,
原方程化为
或
或
解得-
≤x≤
,
所以原方程的解集为{x|-
≤x≤
}
|

(Ⅱ)由已知得:f(x)+g(x)=|2x+1|+|2x-5|=6,
而f(x)+g(x)=
|
原方程化为
|
|
|
解得-
| 1 |
| 2 |
| 5 |
| 2 |
所以原方程的解集为{x|-
| 1 |
| 2 |
| 5 |
| 2 |
点评:含绝对值函数、方程或不等式问题,一般是根据绝对值的意义先把绝对值符号去掉,然后分段研究其性质,画图象,解方程和不等式.

练习册系列答案
相关题目
已知各项均为正数的等比数列{an}公比q≠1,则a3+a7与2a5的大小关系为( )
| A、a3+a7>2a5 |
| B、a3+a7<2a5 |
| C、a3+a7=2a5 |
| D、a3+a7与2a5的大小关系不确定 |
若θ=-5,则角θ的终边在第( )象限.
| A、四 | B、三 | C、二 | D、一 |
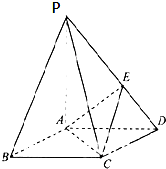 如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=