题目内容
已知函数f(x)=xlnx.
(l)求f(x)的单调区间和极值;
(2)若对任意x∈(0,+∞),f(x)≥
恒成立,求实数m的最大值.
(l)求f(x)的单调区间和极值;
(2)若对任意x∈(0,+∞),f(x)≥
| -x2+mx-3 |
| 2 |
考点:利用导数研究函数的单调性,函数恒成立问题
专题:导数的综合应用
分析:(l)求函数的导数,利用函数单调性和极值之间的关系即可求f(x)的单调区间和极值;
(2)利用不等式恒成立,进行参数分离,利用导数即可求出实数m的最大值.
(2)利用不等式恒成立,进行参数分离,利用导数即可求出实数m的最大值.
解答:
解 (1)∵f(x)=xlnx,
∴f'(x)=lnx+1,
∴f'(x)>0有 x>
,∴函数f(x)在(
,+∞)上递增,f'(x)<0有 0<x<
,
∴函数f(x)在(0,
)上递减,
∴f(x)在x=
处取得极小值,极小值为f(
)=-
.
(2)∵2f(x)≥-x2+mx-3
即mx≤2x•lnx+x2+3,又x>0,
∴m≤
,
令h(x)=
,
h′(x)=
=
令h'(x)=0,解得x=1或x=-3(舍)
当x∈(0,1)时,h'(x)<0,函数h(x)在(0,1)上递减
当x∈(1,+∞)时,h'(x)>0,函数h(x)在(1,+∞)上递增,
∴h(x)min=h(1)=4.
∴a≤4,
即m的最大值为4.
∴f'(x)=lnx+1,
∴f'(x)>0有 x>
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
∴函数f(x)在(0,
| 1 |
| e |
∴f(x)在x=
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
(2)∵2f(x)≥-x2+mx-3
即mx≤2x•lnx+x2+3,又x>0,
∴m≤
| 2x•lnx+x2+3 |
| x |
令h(x)=
| 2x•lnx+x2+3 |
| x |
h′(x)=
| (2x•lnx+x2+3)′•x-(2x•lnx+x2+3)•x′ |
| x2 |
| 2x+x2-3 |
| x2 |
令h'(x)=0,解得x=1或x=-3(舍)
当x∈(0,1)时,h'(x)<0,函数h(x)在(0,1)上递减
当x∈(1,+∞)时,h'(x)>0,函数h(x)在(1,+∞)上递增,
∴h(x)min=h(1)=4.
∴a≤4,
即m的最大值为4.
点评:本题主要考查函数单调性和极值的求解,利用函数单调性,极值和导数之间的关系是解决本题的关键.将不等式恒成立转化为求函数的最值是解决不等式恒成立问题的基本方法.

练习册系列答案
相关题目
定义在(0,+∞)上的可导函数f(x)满足:xf′(x)<f(x)且f(2)=0,则f(x)<0的解集为( )
| A、(0,2) |
| B、(0,2)∪(2,+∞) |
| C、(2,+∞) |
| D、ϕ |
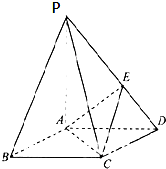 如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=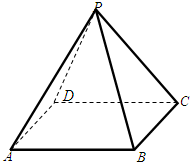 在正四棱锥P-ABCD中,PA=2,直线PA与平面ABCD所成的角为60°.
在正四棱锥P-ABCD中,PA=2,直线PA与平面ABCD所成的角为60°.