题目内容
11．$\underset{lim}{x→∞}$（$\frac{x+3}{x+1}$）2x+2的值为e4．分析 根据极限运用规律求解．
解答 解：$\underset{lim}{x→∞}$（$\frac{x+3}{x+1}$）2x+2=$\underset{lim}{x→∞}$[（1+$\frac{2}{x+1}$）${\;}^{\frac{x+1}{2}}$]4=e4
点评 本题考查了极限的计算，属于中档题，关键记住常见的极限规律．
练习册系列答案
相关题目
19．若集合A={x∈R|x2-3x≤0}，B={0，1，2}，则A∩B=（ ）
| A． | {x|0≤x≤3} | B． | {1，2} | C． | {0，1，2} | D． | {0，1，2，3} |
3．“α=$\frac{π}{4}$”是“tanα=1”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
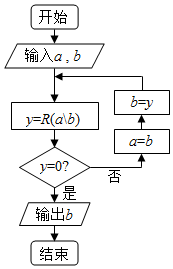“辗转相除法”的算法思路如图所示，记R（a\b）为a除以b所得的余数（a，b∈N*），执行如图的程序框图，若输入a，b分别为405，75，则输出b的值为（ ）