题目内容

19．若集合A={x∈R|x2-3x≤0}，B={0，1，2}，则A∩B=（　　）
A．{x|0≤x≤3}B．{1，2}C．{0，1，2}D．{0，1，2，3}

分析 求出A中不等式的解集确定出A，找出A与B的交集即可．

解答 解：由A中不等式变形得：x（x-3）≤0，
解得：0≤x≤3，即A={x|0≤x≤3}，
∵B={0，1，2}，
∴A∩B={0，1，2}，
故选：C．

点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案
相关题目
9．已知双曲线C：$\frac{{x}^{2}}{a}$-$\frac{{y}^{2}}{4}$=1（a＞0），的离心率为$\frac{\sqrt{13}}{3}$，右焦点为F，点F在渐近线上的射影为M，O为坐标原点，则$\overrightarrow{OF}$$•\overrightarrow{MF}$=4．
10．如图，在三棱柱FPE-ACB中，AC=BC=2，∠ACB=90°．△PAB为等边三角形，PC⊥BC．
（I）求证：平面PBC⊥平面ABC；
（Ⅱ）求二面角B-AP-C的正弦值；并求三棱锥p-ABC的体积．
7．已知参数方程为$\left\{\begin{array}{l}x={x_0}+tcosθ\\ y=tsinθ\end{array}\right.$（t为参数）的直线l经过椭圆$\frac{x^2}{3}+{y^2}=1$的左焦点F1，且交y轴正半轴于点C，与椭圆交于两点A、B（点A位于点C上方）．
（I）求点C对应的参数tC（用θ表示）；
（Ⅱ）若|F1B|=|AC|，求直线l的倾斜角θ的值．
14．已知实数x，y满足$\left\{\begin{array}{l}x-y+1≥0\\ x-3y-1≤0\\ x≤1\end{array}\right.$，若z=kx-y的最小值为-5，则实数k的值为（　　）
A．-3B．3或-5C．-3或-5D．±3
4．已知等比数列{an}的前n项和为Sn，若a2=12，a3•a5=4，则下列说法正确的是（　　）
A．{an}是单调递减数列B．{Sn}是单调递减数列
C．{a2n}是单调递减数列D．{S2n}是单调递减数列
11．$\underset{lim}{x→∞}$（$\frac{x+3}{x+1}$）2x+2的值为e4．
8．在△ABC中，内角A，B，C所对的边分别为a，b，c，且sinA=$\frac{\sqrt{10}}{10}$，sinB=$\frac{\sqrt{5}}{5}$，C为钝角．
（Ⅰ）求A+B的值；
（Ⅱ）若bc=$\sqrt{10}$，求a，b，c的值．
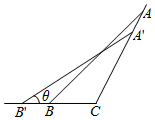9．在△ABC中，角A、B、C所对的边分别是a、b、c．若∠C=$\frac{2}{3}$π，a、b、c依次成等差数列，且公差为2，如图．A′B′分别在射线CA，CB上运动，且满足A′B′=AB，设∠A′B′C′=θ，则△A′CB′周长最大值为7+$\frac{14\sqrt{3}}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网