题目内容
3.设偶函数f(x)满足f(x)=x3-8(x≥0),则{x|f(x-2)>0}=( )| A. | {x|x<-2或x>4} | B. | {x|x<0或x>4} | C. | { x|x<0或x>6} | D. | { x|x<-2或x>5} |
分析 依题意,通过对x-2≥0与x-2<0的讨论,解不等式f(x-2)>0即可求得答案.
解答 解:当x-2≥0,即x≥2时,
联立f(x-2)=(x-2)3-8>0得:x>4;
∵y=f(x)为偶函数,
∴当x-2<0,即x<2时,f(x-2)=f(2-x)=(2-x)3-8,
由(2-x)3-8>0得:x<0;
综上所述,原不等式的解集为:{x|x<0或x>4}.
故选:B.
点评 本题考查指数不等式的解法,着重考查偶函数性质与指数函数的性质的综合应用,属于中档题.

练习册系列答案
相关题目
11.已知当x=$\frac{π}{4}$时,函数f(x)=sin(x+φ)取得最小值,则函数y=f($\frac{3π}{4}$-x)( )
| A. | 是奇函数且图象关于点($\frac{π}{2}$,0)对称 | B. | 是偶函数且图象关于点(π,0)对称 | ||
| C. | 是奇函数且图象关于直线x=$\frac{π}{2}$对称 | D. | 是偶函数且图象关于直线x=π对称 |
12.在直角△ABC中,斜边AC=1,∠BAC=30°,将直角△ABC绕直角边AB旋转一周所形成的几何体的体积为( )
| A. | $\frac{{\sqrt{3}}}{24}π$ | B. | $\frac{{\sqrt{3}}}{8}π$ | C. | $\frac{1}{16}π$ | D. | $\frac{1}{8}π$ |
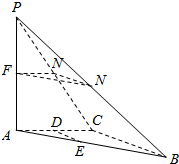 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN⊥PC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN⊥PC.