题目内容
平面向量
=(
,1),
=(-2
,2),则
与
的夹角是 .
| a |
| 3 |
| b |
| 3 |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设
与
夹角为θ,由两个向量的夹角公式得 cosθ=
,把向量的模代入,并利用两个向量的数量积公式化简运算.
| a |
| b |
| ||||
|
|
解答:
解:设
与
夹角为θ,
由两个向量的夹角公式得cosθ=
=
=-
,
∴θ=120°
故答案为:120°.
| a |
| b |
由两个向量的夹角公式得cosθ=
| ||||
|
|
-2
| ||||
|
| 1 |
| 2 |
∴θ=120°
故答案为:120°.
点评:本题考查两个向量的夹角公式的应用,以及两个向量的数量积公式的应用.

练习册系列答案
相关题目
如图,正方体ABCD-A1B1C1D1中,异面直线BC1和CD1所成角为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
一组数据中每个数据都减去50构成一组新数据,则这组新数据的平均数是1.2,方差是4.4,则原来一组数的方差为( )
| A、3.2 | B、4.4 |
| C、4.8 | D、5.6 |
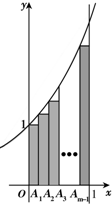 如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于
如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于