题目内容
设数列{an},{bn}满足a1=b1,且对任意正整数n,{an}中小于等于n的项数恰为bn;{bn}中小于等于n的项数恰为an.
(1)求a1;
(2)求数列{an}的通项公式.
(1)首先,容易得到一个简单事实:{an}与{bn}均为不减数列且an∈N,bn∈N.
若a1=b1=0,故{an}中小于等于1的项至少有一项,从而b1≥1,这与b1=0矛盾.
若a1=b1≥2,则{an}中没有小于或等于1的项,从而b1=0,这与b1≥2矛盾.
所以,a1=1.
(2)假设当n=k时,ak=bk=k,k∈N*.
若ak+1≥k+2,因{an}为不减数列,故{an}中小于等于k+1的项只有k项,
于是bk+1=k,此时{bn}中小于等于k的项至少有k+1项(b1,b2,…,bk,bk+1),
从而ak≥k+1,这与假设ak=k矛盾.
若ak+1=k,则{an}中小于等于k的项至少有k+1项(a1,a2,…,ak,ak+1),
于是bk≥k+1,这与假设bk=k矛盾.
所以,ak+1=k+1.
所以,当n=k+1时,猜想也成立.
综上,由(1),(2)可知,an=bn=n对一切正整数n恒成立.
所以,an=n,即为所求的通项公式.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 ,母线与轴的夹角为
,母线与轴的夹角为 ,则这个圆台的高为____________.
,则这个圆台的高为____________.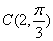 ,半径为2. 以极点为原点,极轴为
,半径为2. 以极点为原点,极轴为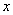 的正半轴,取相同的长度单位建立平面直角坐标系,直线
的正半轴,取相同的长度单位建立平面直角坐标系,直线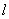 的参数方程为
的参数方程为 (
(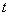 为参数)
为参数)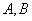 ,
, 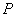 ,求
,求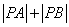
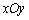 ,圆
,圆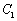 :
: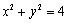 ,圆
,圆 :
: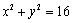 ,点
,点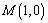 ,动点P、Q
,动点P、Q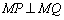 ,则线段
,则线段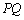 的取值范围是 .
的取值范围是 . 、
、 是圆
是圆 的两条弦,直线
的两条弦,直线 ,求线段
,求线段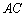 的长度.
的长度.

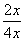 = kx + 1-2k(k为实数)有三个实数解,则这三个实数解的和 _ .
= kx + 1-2k(k为实数)有三个实数解,则这三个实数解的和 _ .  是三个不同的平面,则下列命题中正确的是( )
是三个不同的平面,则下列命题中正确的是( ) B.若
B.若
 D.若
D.若
 .
.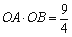 (其中 O为坐标原点).
(其中 O为坐标原点).