题目内容
已知抛物线E:y2=2px(p>0)的准线与x轴交于点K,过点K作圆C:(x-2)2+y2=1的两条切线,切点为M,N,|MN|= .
.
(1)求抛物线E的方程;
(2)设A、B是抛物线E上分别位于x轴两侧的两个动点,且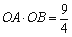 (其中 O为坐标原点).
(其中 O为坐标原点).
①求证:直线AB必过定点,并求出该定点Q的坐标;
②过点Q作AB的垂线与抛物线交于G、D两点,求四边形AGBD面积的最小值.
解:(1)由已知得K(- ,0),C(2,0).
,0),C(2,0).
设MN与x轴交于点R,由圆的对称性可知,|MR|= .
.
 由
由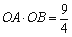 得:
得: 或
或 (舍去),
(舍去),
即 ,所以直线AB过定点
,所以直线AB过定点 ;…………………7分
;…………………7分
(ⅱ)由(ⅰ)得 ,
,
同理得,
则四边形AGBD面积


令 ,则
,则 是关于
是关于 的增函数,
的增函数,
故 .当且仅当
.当且仅当 时取到最小值88 …………………12分
时取到最小值88 …………………12分

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 的光线经
的光线经 轴上点
轴上点 反射后,经过不等式组
反射后,经过不等式组 所表示的区域,则
所表示的区域,则 的取值范围 ;
的取值范围 ;  中,若满足
中,若满足 (
( ,d 为常数),称
,d 为常数),称 则
则
 B.
B. C.
C. D.
D.
 ,定义:
,定义: 的“正弦方差”,则集合
的“正弦方差”,则集合 的“正弦方差”为 。
的“正弦方差”为 。 的最大值是( )
的最大值是( )
 D.-1
D.-1 时,求函数y=x+
时,求函数y=x+ 的最大值.
的最大值.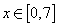 时,输出的y的取值范围是( )
时,输出的y的取值范围是( )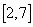 (B)
(B)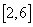 (C)
(C)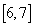 (D)
(D) 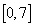
 四点在同一圆上,
四点在同一圆上, 与
与 的延长线交于点
的延长线交于点 ,点
,点 在
在 的延长线上.
的延长线上. ,求
,求 的值;
的值; ,证明:
,证明: .
.