题目内容
在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x-3)2+(y-4)2=1.
(Ⅰ)判断圆C1与圆C2的位置关系;
(Ⅱ)若动圆C同时平分圆C1的周长、圆C2的周长,则动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
(Ⅰ)判断圆C1与圆C2的位置关系;
(Ⅱ)若动圆C同时平分圆C1的周长、圆C2的周长,则动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(Ⅰ)求出两圆的圆心距离,即可判断圆C1与圆C2的位置关系;
(Ⅱ)根据圆C同时平方圆周,建立条件方程即可得到结论.
(Ⅱ)根据圆C同时平方圆周,建立条件方程即可得到结论.
解答:
解:(Ⅰ)C1:(x+1)2+y2=1的圆心为(-1,0),半径r=1,圆C2:(x-3)2+(y-4)2=1的圆心为(3,4),半径R=1,
则|C1C2|=
=
=4
>1+1,
∴圆C1与圆C2的位置关系是相离.
(Ⅱ)设圆心C(x,y),由题意得CC1=CC2,
即
=
,
整理得x+y-3=0,
即圆心C在定直线x+y-3=0上运动.
设C(m,3-m),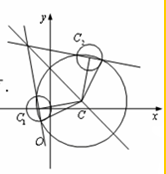
则动圆的半径
=
,
于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,
整理得:x2+y2-6y-2-2m(x-y+1)=0.
由
,
解得
或
,
即所求的定点坐标为(1-
,2-
),(1+
,2+
).
则|C1C2|=
| (-1-3)2+42 |
| 32 |
| 2 |
∴圆C1与圆C2的位置关系是相离.
(Ⅱ)设圆心C(x,y),由题意得CC1=CC2,
即
| (x+1)2+y2 |
| (x-3)2+(y-4)2 |
整理得x+y-3=0,
即圆心C在定直线x+y-3=0上运动.
设C(m,3-m),

则动圆的半径
| 1+(CC1)2 |
| 1+(m+1)2+(3-m)2 |
于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,
整理得:x2+y2-6y-2-2m(x-y+1)=0.
由
|
解得
|
|
即所求的定点坐标为(1-
3
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
点评:本题主要考查圆与圆的位置关系的判断,以及与圆有关的综合应用,考查学生的计算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
直线
x+y-1=0的倾斜角为( )
| 3 |
| A、600 |
| B、1200 |
| C、300 |
| D、1500 |
复数2+2i的虚部是( )
| A、2i | B、2 | C、-2i | D、-2 |