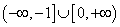题目内容
已知抛物线 ,直线
,直线 ,
,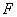 是抛物线的焦点.
是抛物线的焦点.
(1)在抛物线上求一点 ,使点
,使点 到直线
到直线 的距离最小;
的距离最小;
(2)如图,过点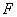 作直线交抛物线于A、B两点.
作直线交抛物线于A、B两点.
①若直线AB的倾斜角为 ,求弦AB的长度;
,求弦AB的长度;
②若直线AO、BO分别交直线 于
于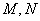 两点,求
两点,求 的最小值.
的最小值.

(1)数形结合,找出与 与平行的切线的切点即为P.(2)易得直线方程
与平行的切线的切点即为P.(2)易得直线方程 ,与抛物线联立,利用弦长公式,可求AB;②设
,与抛物线联立,利用弦长公式,可求AB;②设 ,可得AO,BO方程,与抛物线联立
,可得AO,BO方程,与抛物线联立
试题解析:
解:(1)设 ,
, ,
,
由题可知:

同理由 9分
9分
所以
 ① 10分
① 10分
设 ,由
,由 ,
,

所以此时 的最小值是
的最小值是 ,此时
,此时 ,
, ; 13分
; 13分
综上: 的最小值是
的最小值是 。 14分
。 14分

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目

 ,函数
,函数 的导函数
的导函数 ,且
,且 ,其中
,其中 为自然对数的底数.
为自然对数的底数. 的极值;
的极值; ,使得不等式
,使得不等式 成立,试求实数
成立,试求实数 的取值范围;
的取值范围; 时,对于
时,对于 ,求证:
,求证: .
.  是首项为
是首项为 ,公差为
,公差为 的等差数列,若数列
的等差数列,若数列 是等比数列,则其公比为( )
是等比数列,则其公比为( ) B.
B. C.
C.
 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为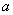 、
、 、
、 ,已知
,已知 (
( ),且
),且 .
. ,
, 时,求
时,求 的取值范围.
的取值范围.
 的体积为
的体积为 
 则满足
则满足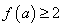 的实数a的取值范围是
的实数a的取值范围是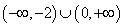 B.
B.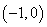
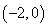 D.
D.