题目内容
已知函数 ,函数
,函数 的导函数
的导函数 ,且
,且 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(1)求 的极值;
的极值;
(2)若 ,使得不等式
,使得不等式 成立,试求实数
成立,试求实数 的取值范围;
的取值范围;
(3)当 时,对于
时,对于 ,求证:
,求证: .
.

当 时,
时, ,若
,若 时,
时, ;若
;若 时,
时,
 存在极大值,且当
存在极大值,且当 时,
时,
综上可知:当 时,
时, 没有极值;当
没有极值;当 时,
时, 存在极大值,且当
存在极大值,且当 时,
时, 4分
4分
(2)  函数
函数 的导函数
的导函数 ,
,

 ,
,
 ,
, 5分
5分


 当
当 时,
时, ,
, 在
在 上为减函数;当
上为减函数;当 时,
时, ,
, 在
在 上为增函数,
上为增函数,

 ,
, ,
,
由于 在
在 上为增函数,
上为增函数,

 14分
14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 、
、 是不同的两条直线,
是不同的两条直线, 、
、 是不同的两个平面,分析下列命题,其中正确的是( ).
是不同的两个平面,分析下列命题,其中正确的是( ). ,
, ,
, B.
B.
 ,
, D.
D. ,
,
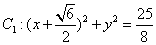 ,圆
,圆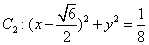 ,动圆
,动圆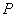 与已知两圆都外切.(1)求动圆的圆心
与已知两圆都外切.(1)求动圆的圆心 的方程;(2)直线
的方程;(2)直线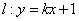 与点
与点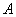 、
、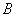 ,
,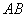 的中垂线与
的中垂线与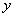 轴交于点
轴交于点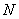 ,求点
,求点 对
对 ,都有
,都有 ,则
,则 是____________________.
是____________________. -
-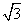 sin x.
sin x. =
= ,求
,求 的值.
的值. =1-yi,则x+yi=( )
=1-yi,则x+yi=( ) ,则
,则 的取值范围是( )
的取值范围是( ) B.
B.  C.
C. D.
D.
 ,直线
,直线 ,
,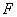 是抛物线的焦点.
是抛物线的焦点. ,使点
,使点 的距离最小;
的距离最小; ,求弦AB的长度;
,求弦AB的长度;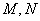 两点,求
两点,求 的最小值.
的最小值.
 ,方程
,方程 的两根为
的两根为 .
. ;
;
 =
= 的图像与
的图像与 轴交于A,B两点,求|AB|长度的取值范围。
轴交于A,B两点,求|AB|长度的取值范围。