题目内容
8.5人从左至右排成一行,甲排在中间的不同方法种数有( )| A. | 12 | B. | 24 | C. | 36 | D. | 120 |
分析 根据题意,分2步进行分析:①分析甲,甲必须排在中间,有1种情况,②分析其他4个人,将剩余的4个人排在除中间之外的4个位置,由排列数公式计算可得其排法数目;由分步计数原理计算可得答案.
解答 解:根据题意,分2步进行分析:
①甲必须排在中间,有1种情况,
②将剩余的4个人排在除中间之外的4个位置,有A44=24种排法;
则甲排在中间的不同方法种数有1×24=24种;
故选:B.
点评 本题考查排列、组合的运用,涉及分步计数原理的应用,注意要先满足甲排在中间的要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知z=2+i,(i是虚数单位),z的共轭复数是$\overline z$,则复数$\frac{\overline z}{i}$=( )
| A. | -1-2i | B. | 1-2i | C. | -1+2i | D. | 1+2i |
19.若α是第二象限角,且sinα=$\frac{3}{5}$,则cosα=( )
| A. | $\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
3.函数y=lg(x2-4)+$\sqrt{{x}^{2}+6x}$的定义域是( )
| A. | (-∞,-2)∪[0,+∞) | B. | (-∞,-6]∪(2,+∞) | C. | (-∞,-2]∪[0,+∞) | D. | (-∞,-6)∪[2,+∞) |
17.在△ABC中,若sin(B+C)=2sinBcosC,那么这个三形一定是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰三角形 |
 设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.
设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.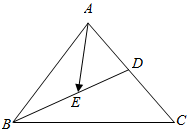 如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.
如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.