题目内容
 如图,椭圆E:
如图,椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(l)求椭圆E的方程;
(2)设t∈R且t≠0,过点M(4,t)的直线MA,MB与椭圆E分别交于点P,Q.求证:点P,F,Q共线.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件知
=
,所以设E的方程设为
+
=1,再由当x0=2c时,|HF|min=c=1,能求出椭圆E的方程.
(2)由A(-2,0),B(2,0),过点M(4,t)的直线MA,MB与椭圆E分别交于点P,Q,设MA的方程为y=
(x+2),联立方程组
,得(27+t2)x2+4t
x+(4t2-108)=0,由此能证明t∈R,且t≠0,点P、F、Q三点共线.
| c |
| a |
| 1 |
| 2 |
| x2 |
| 4c2 |
| y2 |
| 3c2 |
(2)由A(-2,0),B(2,0),过点M(4,t)的直线MA,MB与椭圆E分别交于点P,Q,设MA的方程为y=
| t |
| 6 |
|
| 2 |
解答:
(1)解:由椭圆E的离心率为
,得
=
,即a=2c,
∴b2=a2-c2=3c2,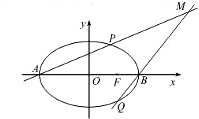
∴E的方程设为
+
=1,
设椭圆上的动点H(x0,y0),(-2c≤x0≤2c),
∵F(c,0),∴|HF|=
,①
又由
+
=1,即y02=3c2-
x02,②
②代入①整理,得|HF|=
,(-2c≤x0≤2c),
∴当x0=2c时,|HF|min=c=1
∴所求椭圆E的方程为
+
=1.
(2)证明:由(1)知A(-2,0),B(2,0),
∵过点M(4,t)的直线MA,MB与椭圆E分别交于点P,Q,
∴kMA=
,kMB=
,
∴MA的方程为y=
(x+2),
联立方程组
,得(27+t2)x2+4t
x+(4t2-108)=0,
∴xA+xP=
,
∴xP=
-xA=
,
代入MA的方程,得yP=
(xP+2)=
,
∴点P(
,
),
同理,求得点Q(
,
),
∴
=(
,
),
=(
,
),
即
=
,
∴t∈R,且t≠0,点P、F、Q三点共线.
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
∴b2=a2-c2=3c2,

∴E的方程设为
| x2 |
| 4c2 |
| y2 |
| 3c2 |
设椭圆上的动点H(x0,y0),(-2c≤x0≤2c),
∵F(c,0),∴|HF|=
| (x0-c)2+y02 |
又由
| x02 |
| 4c2 |
| y02 |
| 3c2 |
| 3 |
| 4 |
②代入①整理,得|HF|=
|
∴当x0=2c时,|HF|min=c=1
∴所求椭圆E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)证明:由(1)知A(-2,0),B(2,0),
∵过点M(4,t)的直线MA,MB与椭圆E分别交于点P,Q,
∴kMA=
| t |
| 6 |
| t |
| 2 |
∴MA的方程为y=
| t |
| 6 |
联立方程组
|
| 2 |
∴xA+xP=
| -4t2 |
| 27+t2 |
∴xP=
| -4t2 |
| 27+t2 |
| 54-2t2 |
| 27+t2 |
代入MA的方程,得yP=
| t |
| 6 |
| 18t |
| 27+t2 |
∴点P(
| 54-2t2 |
| 27+t2 |
| 18t |
| 27+t2 |
同理,求得点Q(
| 2t2-6 |
| 3+t2 |
| -6t |
| 3+t2 |
∴
| PF |
| 3t2-27 |
| 27+t2 |
| -18t |
| 27+t2 |
| FQ |
| t2-9 |
| 3+t2 |
| -6t |
| 3+t2 |
即
| PF |
| 27+t2 |
| 3(3+t2) |
| FQ |
∴t∈R,且t≠0,点P、F、Q三点共线.
点评:本题考查椭圆的方程的求法,考查直线与椭圆的位置关系,考查代数法求方程的解,考查数形结合、运算求解、转化与化归以及分析与解决问题的能力.

练习册系列答案
相关题目
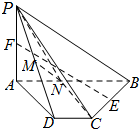 如图所示,四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,∠ABC=90°,AP=BC=2,AB=3,CD=1,E、F、M分别是BC、PA、PD的中点.
如图所示,四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,∠ABC=90°,AP=BC=2,AB=3,CD=1,E、F、M分别是BC、PA、PD的中点.