题目内容
19.为了解市场上某品牌中性笔替芯的质量情况,现随机抽取100支进行研究,其中合格品为80支.(1)根据产品质量按分层抽样的方法从这100只中抽取10支,甲,乙同学从抽出的10支中随机取3支,求恰有2支合格的概率.
(2)以随机抽取的100支中合格品的频率作为该产品的合格率,甲乙两同学分别在市场上购得该品牌替芯2支,设两人购得的合格品数分别为x,y,记随机变量X=|x-y|,求X的分布列及数学期望E(X).
分析 (1)由题意抽出的10支替芯中,合格品有8支,由此能求出甲,乙同学从抽出的10支中随机取3支,恰有2支合格的概率.
(2)由题意,该替芯的合格率P=$\frac{4}{5}$,设Pi表示甲(乙)购得i(i=0,1,2)支合格品的概率,随机变量X的可能取值为0,1,2,分别求出相应的概率,由此能求出随机变量X的分布列和EX.
解答 解:(1)由题意抽出的10支替芯中,合格品有8支,
则甲,乙同学从抽出的10支中随机取3支,恰有2支合格的概率P=$\frac{{C}_{8}^{2}{C}_{2}^{1}}{{C}_{10}^{3}}$=$\frac{7}{15}$.
(2)由题意,该替芯的合格率P=$\frac{4}{5}$,
设Pi表示甲(乙)购得i(i=0,1,2)支合格品的概率,
则P0=($\frac{1}{5}$)2=$\frac{1}{25}$,
P1=2×$\frac{1}{5}×\frac{4}{5}$=$\frac{8}{25}$,
P2=$(\frac{4}{5})^{2}$=$\frac{16}{25}$,
随机变量X的可能取值为0,1,2,
P(X=0)=${{P}_{0}}^{2}+{{P}_{1}}^{2}+{{P}_{2}}^{2}$=$\frac{321}{625}$,
P(X=1)=2P0•P1+2P1P2=$\frac{272}{625}$,
P(X=2)=2P0•P2=$\frac{32}{625}$,
∴随机变量X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{321}{625}$ | $\frac{272}{625}$ | $\frac{32}{625}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意分层抽样的性质的合理运用.

练习册系列答案
相关题目
9.设命题p:?a>1,函数f(x)=xa(x>0)是增函数,则¬p为( )
| A. | ?a0<1,函数f(x)=xa0(x>0)是减函数 | B. | ?a>1,函数f(x)=xa(x>0)不是减函数 | ||
| C. | ?a0>1,函数f(x)=xa(x>0)不是增函数 | D. | ?a>1,函数f(x)=xa(x>0)是减函数 |
10.将函数f(x)=sin(2x+$\frac{π}{4}$)的图象向左平移φ(φ>0)个单位,所得图象关于y轴对称,则φ的最小值为( )
| A. | $\frac{1}{8}$π | B. | $\frac{1}{2}$π | C. | $\frac{3}{4}$π | D. | $\frac{3}{8}$π |
14.已知函数$f(x)=3sin({ωx+\frac{π}{6}})-2({ω>0})$的图象向右平移$\frac{2π}{3}$个单位后与原图象重合,则ω的最小值是( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
11.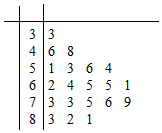 某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意
某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意
(1)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“満意”与“否”与性别有有关?
附:
(2)以此“满意”的频率作为概率,求在3人中恰有2人满意的概率;
(3)从以上男性用户中抽取2人,女性用户中抽取1人,其中满意的人数为ξ,求ξ的分布列与数学期望.
 某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意
某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意(1)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“満意”与“否”与性别有有关?
附:
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(3)从以上男性用户中抽取2人,女性用户中抽取1人,其中满意的人数为ξ,求ξ的分布列与数学期望.
9.函数y=-3sin3x的最大值与取得最大值时相应的一个x的值为( )
| A. | 1,$\frac{π}{2}$ | B. | 1,-$\frac{π}{2}$ | C. | 3,$\frac{π}{6}$ | D. | 3,-$\frac{π}{6}$ |