题目内容
9.设命题p:?a>1,函数f(x)=xa(x>0)是增函数,则¬p为( )| A. | ?a0<1,函数f(x)=xa0(x>0)是减函数 | B. | ?a>1,函数f(x)=xa(x>0)不是减函数 | ||
| C. | ?a0>1,函数f(x)=xa(x>0)不是增函数 | D. | ?a>1,函数f(x)=xa(x>0)是减函数 |
分析 利用全称命题的否定是特称命题,写出结果即可.
解答 解:因为全称命题是否定是特称命题,所以,命题p:?a>1,函数f(x)=xa(x>0)是增函数,则¬p为:?a0>1,函数f(x)=xa(x>0)不是增函数.
故选:C.
点评 本题考查命题的否定,特称命题与全称命题否定关系,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.设Sn是等差数列{an}的前n项和,若$\frac{{S}_{3}}{{S}_{6}}$=$\frac{1}{4}$,则$\frac{{S}_{6}}{{S}_{12}}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
20.执行如图的程序框图,若t输入(a,a+1)中的数值,输出的S是单调增加的,则实数a的取值范围是( )
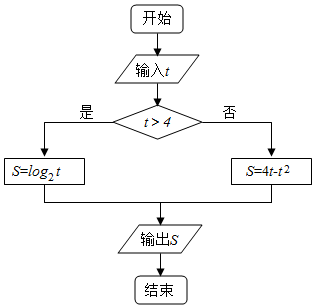

| A. | (-∞,1) | B. | [1,4] | C. | (-∞,1]∪(4,+∞) | D. | (-∞,1]∪[4,+∞) |
17.已知函数f(x)=$\left\{\begin{array}{l}{1+{4}^{x},x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,则f(f($\frac{\sqrt{2}}{4}$))等于( )
| A. | $\frac{9}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{11}{8}$ | D. | $\frac{7}{4}$ |