题目内容
10.将函数f(x)=sin(2x+$\frac{π}{4}$)的图象向左平移φ(φ>0)个单位,所得图象关于y轴对称,则φ的最小值为( )| A. | $\frac{1}{8}$π | B. | $\frac{1}{2}$π | C. | $\frac{3}{4}$π | D. | $\frac{3}{8}$π |
分析 求得y=sin(2x+$\frac{π}{4}$)的图象向左平移φ(φ>0)个单位后的解析式,利用正弦函数的对称性可得φ的最小值.
解答 解:将函数f(x)=sin(2x+$\frac{π}{4}$)的图象向左平移φ(φ>0)个单位,所得图象的解析式为为:f(x)=sin[2(x+φ)+$\frac{π}{4}$]=sin(2x+2φ+$\frac{π}{4}$),
其图象关于y轴对称,可得当x=0时,函数取得最值,
可得:2φ+$\frac{π}{4}$=kπ$+\frac{π}{2}$,k∈Z,
解得:φ=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z,当k=0时,φ取得最小正值为$\frac{1}{8}π$.
故选:A.
点评 本题考查函数y=Asin(ωx+φ)的图象变换,求得函数图象平移后的解析式是关键,考查综合分析与运算能力,属于中档题.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
20.执行如图的程序框图,若t输入(a,a+1)中的数值,输出的S是单调增加的,则实数a的取值范围是( )
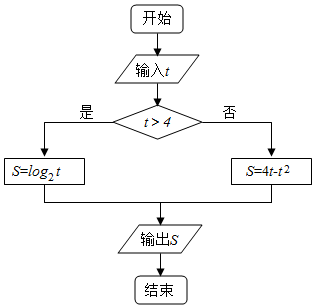

| A. | (-∞,1) | B. | [1,4] | C. | (-∞,1]∪(4,+∞) | D. | (-∞,1]∪[4,+∞) |