题目内容
7.为了解重庆某社区居民的家庭年收入和年支出的关系,随机调查了5户家庭,得到统计数据表,根据表中可得回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=0.5,据此估计,该社区一户收入为16万元家庭年支出为( )| 收入x(万元) | 6 | 8 | 10 | 12 | 14 |
| 支出y(万元) | 6 | 7 | 8 | 9 | 10 |
| A. | 15万元 | B. | 14万元 | C. | 11万元 | D. | 10万元 |
分析 计算样本中心,代入回归方程解出$\stackrel{∧}{a}$,得出回归方程,利用回归方程进行预测.
解答 解:$\overline{x}$=10,$\overline{y}$=8.
∴$\stackrel{∧}{a}$=8-0.5×10=3.
所以回归方程为:$\stackrel{∧}{y}$=0.5x+3,
当x=16时,$\stackrel{∧}{y}$=0.5×16+3=11.
故选C.
点评 本题考查了线性回归方程的性质及利用回归方程进行数值预测,属于基础题.

练习册系列答案
相关题目
17.已知A,B是单位圆上的两点,O为圆心,且∠AOB=90°,MN是圆O的一条直径,点C在圆内,且满足$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$(λ∈R),则$\overrightarrow{CM}$•$\overrightarrow{CN}$的最小值为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | -1 |
15.在平面直角坐标系中,若角α的顶点与原点重合,始边与x轴的非负半轴重合,终边过点P(-$\sqrt{3}$,-1),则sin($\frac{π}{2}$-α)=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
12.已知(1-x)10=a0+a1(1+x)+a2(1+x)2+…+a10(1+x)10,则a9=( )
| A. | -20 | B. | 20 | C. | -10 | D. | 10 |
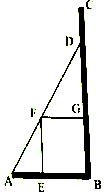 如图欲在直角区域ABC内的空地上植造一块“绿地Rt△ABD”,D在BC边上.其中AB=1,设BD=x(x>0)且BC足够长,规划在△ABD的内接正方形BEFG内种花,其余地方种草,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“完美度”.
如图欲在直角区域ABC内的空地上植造一块“绿地Rt△ABD”,D在BC边上.其中AB=1,设BD=x(x>0)且BC足够长,规划在△ABD的内接正方形BEFG内种花,其余地方种草,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“完美度”.