题目内容
4．已知f（logax）=log${\;}_{a}^{2}$x-alogax2+1（a＞0且a≠1）．（1）求y=f（x）的解析式及其定义域；
（2）若函数y=f（x）-a在（0，1）内有且只有一个零点，求a的取值范围．
分析 （1）令logax=t，换元可得；
（2）令g（x）=x2-2ax+1-a，问题等价于g（0）g（1）＜0或$\left\{\begin{array}{l}{0＜-\frac{-2a}{2}＜1}\\{△=4{a}^{2}-4（1-a）=0}\end{array}\right.$，解不等式组可得a的范围．
解答 解：（1）令logax=t，换元可得f（t）=t2-2at+1，
∴y=f（x）的解析式为f（x）=x2-2ax+1，定义域为R；
（2）∵函数y=x2-2ax+1-a在（0，1）内有且只有一个零点，
令g（x）=x2-2ax+1-a，则g（0）g（1）＜0或$\left\{\begin{array}{l}{0＜-\frac{-2a}{2}＜1}\\{△=4{a}^{2}-4（1-a）=0}\end{array}\right.$，
解得a=$\frac{\sqrt{5}-1}{2}$或$\frac{2}{3}$＜a＜1
点评 本题考查对数函数的图象和性质，涉及函数零点的判定，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
15．已知集合M={1，2，3}，N={2，3，4，5}，那么M∩N=（ ）
| A． | ∅ | B． | {1，4，5} | C． | {1，2，3，4，5} | D． | {2，3} |
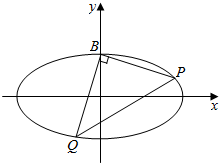如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率是$\frac{{\sqrt{3}}}{2}$，一个顶点是B（0，1）．