题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{2x-{x}^{2},x>0}\\{0,x=0}\\{{x}^{2}+mx,x<0}\end{array}\right.$是奇函数,(1)求实数m的值;
(2)画出函数y=f(x)的图象(不用列表),并根据图象写出该函数的单调区间;
(3)若函数y=f(x)在区间[-1,a-2]上单调递增,求实数a的取值范围.
分析 (1)由已知中函数的解析式,先求出f(1),再由f(-1)=-f(1)得到f(-1)以及m的值;
(2)由已知中函数的解析式,结合二次函数的图象和性质,可得y=f(x)的图象,数形结合可写出单调区间;
(3)要使f(x)在[-1,a-2]上单调递增,结合f(x)的图象知$\left\{\begin{array}{l}{a-2>-1}\\{a-2≤1}\end{array}\right.$,由此求得a的范围.
解答 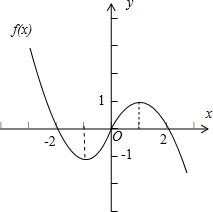 解:(1)设x<0,则-x>0,
解:(1)设x<0,则-x>0,
所以,f(-x)=-(-x)2+2(-x)=-x2-2x.
又f(x)为奇函数,所以f(-x)=-f(x),
于是x<0时,f(x)=x2+2x=x2+mx,所以m=2,
(2)如图所示,由图可得:
f(x)的单调递增区间(-1,1),
f(x)的单调递减区间(-∞,-1),(1,+∞);
(3)要使f(x)在[-1,a-2]上单调递增,
结合f(x)的图象知$\left\{\begin{array}{l}{a-2>-1}\\{a-2≤1}\end{array}\right.$,
解得1<a≤3,故实数a的取值范围是(1,3].
点评 本题主要考查利用函数的奇偶性求函数的解析式,作函数的图象,函数的单调性的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列函数中,既是奇函数又是增函数的是( )
| A. | $y={x^{\frac{1}{2}}}$ | B. | y=x3 | C. | $y={({\frac{1}{2}})^x}$ | D. | y=|x-1| |
10.已知函数f(x)=$\left\{\begin{array}{l}{{a}^{x}(x<0)}\\{(3-a)x+\frac{1}{2}a(x≥0)}\end{array}\right.$是增函数,则a的取值范围是( )
| A. | (1,2) | B. | (1,3) | C. | (2,3) | D. | [2,3) |
14.设集合A={x|x<2},则( )
| A. | ∅∈A | B. | $\sqrt{3}∉A$ | C. | $\sqrt{3}∈A$ | D. | $\sqrt{3}$$\underset{?}{≠}$A |
15.若函数y=aex+3x在R上有小于零的极值点,则实数a的取值范围是( )
| A. | (-3,+∞) | B. | (-∞,-3) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,-$\frac{1}{3}$) |