题目内容
15.若函数y=aex+3x在R上有小于零的极值点,则实数a的取值范围是( )| A. | (-3,+∞) | B. | (-∞,-3) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,-$\frac{1}{3}$) |
分析 由题意可知:则y′=aex+3=0有负根,则ex=-$\frac{3}{a}$在y轴的右侧有交点,由函数的性质即可求得实数a的取值范围.
解答 解:y=aex+3x,求导,y′=aex+3,
由若函数y=aex+3x在R上有小于零的极值点,
则y′=aex+3=0有负根,
则a≠0,
则ex=-$\frac{3}{a}$在y轴的左侧有交点,
∴0<-$\frac{3}{a}$<1,解得:a<-3,
实数a的取值范围(-∞,-3)
故选B.
点评 本题考查导数的单调性,极值与导数的关系,考查指数函数的性质,考查转化思想,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6.根据如下样本数据得到的回归方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,若$\stackrel{∧}{a}$=4.5,则x每增加1个单位,y就( )
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 |
| A. | 增加0.9个单位 | B. | 减少0.9个单位 | C. | 增加0.72个单位 | D. | 减少0.72个单位 |
20.若函数f(x)=[x3+3x2+(a+6)x+6-a]e-x在区间(2,4)上存在极大值点,则实数a的取值范围是( )
| A. | (-∞,-32) | B. | (-∞,-27) | C. | (-32,-27) | D. | (-32,-27] |
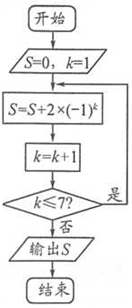 已知某算法的程序框图如图所示,则输出的S的值是-2.
已知某算法的程序框图如图所示,则输出的S的值是-2. 秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=-1,c=1,d=0.1,则输出的x的值为( )
秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=-1,c=1,d=0.1,则输出的x的值为( ) 某高校调查了400名大学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25)[25,27.5),[27.5,30].根据此直方图,这400名大学生中每周的自习时间不少于25小时的人数是120.
某高校调查了400名大学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25)[25,27.5),[27.5,30].根据此直方图,这400名大学生中每周的自习时间不少于25小时的人数是120.