题目内容
18.已知圆与y轴相切,圆心在直线3x-y=0,且这个圆经过点A(2,3),求该圆的方程.分析 由圆心在直线3x-y=0上设出圆心坐标,然后根据圆与y轴相切得到圆心到y轴的距离求出半径,表示出圆的方程,把A代入即可求出.
解答 解:因为圆心在3x-y=0上,所以设圆心坐标为(m,3m)且m>0,根据圆与y轴相切得到半径为m
则圆的方程为(x-m)2+(y-3m)2=m2,把A(2,3)代入圆的方程得:(2-m)2+(3-3m)2=m2,
化简得:9m2-22m+13=0,则m=1或$\frac{13}{9}$,
所以圆的方程为(x-1)2+(y-3)2=1或(x-$\frac{13}{9}$)2+(y-$\frac{13}{3}$)2=$\frac{169}{81}$.
点评 本题考查用待定系数法求圆的方程,一般可通过已知条件,设出所求方程,再寻求方程组进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.正方体ABCD-A1B1C1D1中,截面BA1C1和直线AC的位置关系是( )
| A. | AC∥平面BA1C1 | B. | AC与平面BA1C1相交 | ||
| C. | AC在平面BA1C1内 | D. | 上述答案均不正确 |
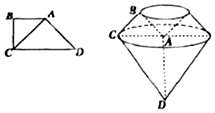 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.