题目内容
(本小题共14分)已知椭圆 的离心率为
的离心率为 ,且过点
,且过点 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)直线 交椭圆于P、Q两点,若点B始终在以PQ为直径的圆内,求实数
交椭圆于P、Q两点,若点B始终在以PQ为直径的圆内,求实数 的取值范围.
的取值范围.
(Ⅰ) (Ⅱ)
(Ⅱ)
【解析】
试题分析:(Ⅰ)由椭圆过点 得
得 ,由离心率是
,由离心率是 得
得 ,另外结合
,另外结合 列方程组即可确定
列方程组即可确定 的值从而得到椭圆C的方程;(Ⅱ)设
的值从而得到椭圆C的方程;(Ⅱ)设 直线
直线 的方程为
的方程为 ,将直线方程与椭圆方程联立消去一个变量,得到关于
,将直线方程与椭圆方程联立消去一个变量,得到关于 的一元二次方程,结合一元二次方程根的判别式与韦达定理以及由点B在以PQ为直径的圆内,得
的一元二次方程,结合一元二次方程根的判别式与韦达定理以及由点B在以PQ为直径的圆内,得 为钝角或平角,即
为钝角或平角,即 确定的关系,从而求出实数
确定的关系,从而求出实数 的取值范围.
的取值范围.
试题解析:(Ⅰ)由题意知 ,解得
,解得 ,
,
椭圆的标准方程为: . 4分
. 4分
(Ⅱ)设
联立 ,消去
,消去 ,得:
,得: 6分
6分
依题意:直线 恒过点
恒过点 ,此点为椭圆的左顶点,
,此点为椭圆的左顶点,
所以 ,
, ----①,
----①,
由(*)式, -------②,
-------②,
可得 ----③, 8分
----③, 8分
由①②③, ,
, 10分
10分
由点B在以PQ为直径的圆内,得 为钝角或平角,即
为钝角或平角,即 .
.


 . 12分
. 12分
即 ,整理得
,整理得 .
.
解得: . 14分
. 14分
考点:椭圆方程,直线与椭圆位置关系

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
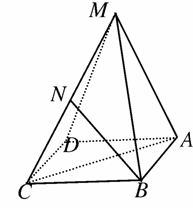
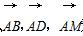 为基向量表示出向量
为基向量表示出向量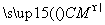 ,并求CM的长;
,并求CM的长; D.2
D.2 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,则
,则 ____________.
____________.
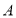 为非空实数集,若
为非空实数集,若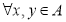 ,都有
,都有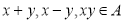 ,则称
,则称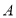 为封闭集.
为封闭集.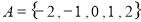 为封闭集;
为封闭集;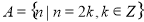 为封闭集;
为封闭集;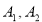 为封闭集,则
为封闭集,则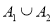 为封闭集;
为封闭集;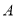 为封闭集,则一定有
为封闭集,则一定有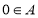 .
.
 B.
B. C.
C. D.
D. 

 ,准线与
,准线与 轴的交点为
轴的交点为 .
. 的方程;
的方程; ,过点
,过点 的直线
的直线 与抛物线
与抛物线 ,AQ与BQ分别与抛物线
,AQ与BQ分别与抛物线 ,
, 的斜率分别为
的斜率分别为 ,问:是否存在常数
,问:是否存在常数 ,使得
,使得 ,
, 的值,若不存在,说明理由.
的值,若不存在,说明理由.