题目内容
函数y=|logax|(0<a<1)的定义域为[m,n](m<n),值域为[0,1],若n-m的最小值为
,则实数a的值为( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都错 |
考点:对数函数的图像与性质
专题:计算题,函数的性质及应用
分析:由|logax|=1得,x=a或x=
,区间n-m的最小值为1-a或
-1,从而讨论求解.
| 1 |
| a |
| 1 |
| a |
解答:
解:由|logax|=1得,x=a或x=
,区间n-m的最小值为1-a或
-1.
(1)当1-a=
时,a=
,此时
-1=
>
,符合题意;
(2)当
-1=
时,a=
,此时1-a=
<
,不符题意.
综上知,a=
,
故选B.
| 1 |
| a |
| 1 |
| a |
(1)当1-a=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| a |
| 1 |
| 3 |
| 1 |
| 4 |
(2)当
| 1 |
| a |
| 1 |
| 4 |
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 4 |
综上知,a=
| 3 |
| 4 |
故选B.
点评:本题考查了对数函数的性质应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,向边长为2的正方形中随机投入一粒黄豆,若圆C的方程为(x-2)2+(y-2)2=
如图,向边长为2的正方形中随机投入一粒黄豆,若圆C的方程为(x-2)2+(y-2)2=| 9 |
| 4 |
A、
| ||
B、1-
| ||
C、1-
| ||
D、
|
某程序框图如图所示,则输出的结果S=( )
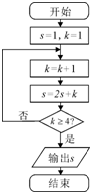

| A、11 | B、26 | C、57 | D、120 |
不等式(x+1)(2-x)>0的解集是( )
| A、(-2,1) |
| B、(-1,2) |
| C、(-∞,-2)∪(1,+∞) |
| D、(-∞,-1)∪(2,+∞) |
不等式x2+2014x-2015>0的解集为( )
| A、{x|-2015<x<1} |
| B、{x|x>1或x<-2015} |
| C、{x|-1<x<2015} |
| D、{x|x<-1或x>2015} |
