题目内容
4.等比数列{an}中,an>0,al+a2=6,a3=8,则a6=( )| A. | 64 | B. | 128 | C. | 256 | D. | 512 |
分析 由已知条件可得首项和公比的方程组,解方程组代入通项公式可得.
解答 解:设等比数列{an}的公比为q,q>0
则al+a2=a1(1+q)=6,a3=a1q2=8,
联立解得q=2,a1=2,
∴a6=2×25=64,
故选:A.
点评 本题考查等比数列的通项公式,求出数列的首项和公比是解决问题的关键,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分的集合为( )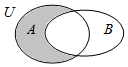

| A. | {x|-1<x<1} | B. | {x|1≤x<3} | C. | {x|x<3} | D. | {x|x≤-1} |
16.命题“?x∈R,f(x)g(x)≠0”的否定是( )
| A. | ?x∈R,f(x)=0且g(x)=0 | B. | ?x∈R,f(x)=0或g(x)=0 | ||
| C. | ?x0∈R,f(x0)=0且g(x0)=0 | D. | ?x0∈R,f(x0)=0或g(x0)=0 |
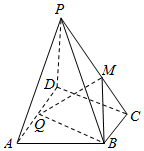 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点. 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=30°,PD⊥平面ABCD,AD=2,点E为AB上一点,且$\frac{AE}{AB}$=m,点F为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=30°,PD⊥平面ABCD,AD=2,点E为AB上一点,且$\frac{AE}{AB}$=m,点F为PD中点.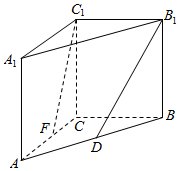 如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.