题目内容
6. 如图,在△ABC中,已知O为边BC的中点,∠A0B=60°,AB=10.
如图,在△ABC中,已知O为边BC的中点,∠A0B=60°,AB=10.(1)当OA=4$\sqrt{3}$时,求△ABC的面积;
(2)设AC=x,求x的取值范围.
分析 (1)利用正弦定理求出B的正弦,进一步求出BC上的高,进一步求出OB的长度,由三角形面积公式求得;
(2)利用正弦定理将OB用角BAO表示,根据角度范围求出OB范围,再由三边关系得到所求.
解答 解:(1)在△AOB中,$\frac{OA}{sinB}=\frac{AB}{sin∠AOB}$,则sinB=$\frac{4\sqrt{3}×\frac{\sqrt{3}}{2}}{10}=\frac{3}{5}$,所以BC边上的高AD=ABsinB=10×$\frac{3}{5}$=6,
所以OB=4$\sqrt{3}$×$\frac{1}{2}$+10×$\frac{3}{5}$=2$\sqrt{3}$+6,所以△ABC的面积2×$\frac{1}{2}$OB×AD=(2$\sqrt{3}$+6)×6=12($\sqrt{3}$+3);
(2)在△AOB中,设∠BAO=α,则$\frac{OB}{sinα}=\frac{AB}{sin60°}$,所以OB=$\frac{20\sqrt{3}}{3}$sinα,又0≤α<120°,又BC=2OB,所以BC≤$\frac{40\sqrt{3}}{3}$,
在△ABC中,BC-AB<AC<AB+BC即$\frac{40\sqrt{3}}{3}-10$<x<$\frac{40\sqrt{3}}{3}+10$.
点评 本题主要考查了利用正弦定理解三角形;属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.在等差数列{an}中,a2、a13是方程x2-x-3=0的两个根,则前14项的和S14为( )
| A. | 20 | B. | 16 | C. | 12 | D. | 7 |
14.已知左、右焦点分别是F1,F2的双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$上一点A满足AF1⊥AF2,且|AF1|=3|AF2|,则该双曲线的渐近线方程为( )
| A. | y=±$\frac{\sqrt{10}}{2}$x | B. | y=±$\frac{\sqrt{6}}{2}$x | C. | y=±$\sqrt{6}$x | D. | y=±$\sqrt{10}$x |
15.已知直线2x+y-10=0过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的焦点且与该双曲线的一条渐近线垂直,则该双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | C. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | D. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ |
 如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AC=1,AA1=2,且P,Q,M分别是BB1,CC1,B1C1的中点,AB⊥AQ.
如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AC=1,AA1=2,且P,Q,M分别是BB1,CC1,B1C1的中点,AB⊥AQ.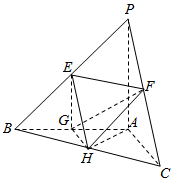 如图,在三棱锥P-ABC中,E、F、G、H分别是棱PB、PC、AB、BC的中点,PA⊥平面ABC,AB⊥AC,PA=AB=AC=2.
如图,在三棱锥P-ABC中,E、F、G、H分别是棱PB、PC、AB、BC的中点,PA⊥平面ABC,AB⊥AC,PA=AB=AC=2.