题目内容
正整数数列{an}满足:a1=1,an+1=
(Ⅰ)写出数列{an}的前5项;
(Ⅱ)将数列{an}中所有值为1的项的项数按从小到大的顺序依次排列,得到数列{nk},试用nk表示nk+1(不必证明);
(Ⅲ)求最小的正整数n,使an=2013.
|
(Ⅰ)写出数列{an}的前5项;
(Ⅱ)将数列{an}中所有值为1的项的项数按从小到大的顺序依次排列,得到数列{nk},试用nk表示nk+1(不必证明);
(Ⅲ)求最小的正整数n,使an=2013.
分析:(Ⅰ)由数列{an}满足递推公式,令n=1,2,3,4及a1=1,我们易得到a2,a3,a4,a5,的值;
(Ⅱ)由(1)和条件可归纳数列{nk}中每一项的值与序号的关系,由归纳推理出nk的一个通项公式,再由(Ⅰ)归纳出数列{an}中项之间的关系式,再得到项数之间的关系式;
(Ⅲ)把(Ⅱ)的结论化为2nk+1+1=3(2nk+1),记2nk+1=xk,转化为新的等比数列{xk},利用此数列的通项公式进而求出nk的表达式,把nk+1=3nk+1转化为不等式“an≤3nk+1=nk+1”,给k具体值结合(Ⅱ)的结论,进行注意验证an与2013的大小关系,一直到n8+2-m=2013,进而求出m的值,代入对应的式子求出n的值.
(Ⅱ)由(1)和条件可归纳数列{nk}中每一项的值与序号的关系,由归纳推理出nk的一个通项公式,再由(Ⅰ)归纳出数列{an}中项之间的关系式,再得到项数之间的关系式;
(Ⅲ)把(Ⅱ)的结论化为2nk+1+1=3(2nk+1),记2nk+1=xk,转化为新的等比数列{xk},利用此数列的通项公式进而求出nk的表达式,把nk+1=3nk+1转化为不等式“an≤3nk+1=nk+1”,给k具体值结合(Ⅱ)的结论,进行注意验证an与2013的大小关系,一直到n8+2-m=2013,进而求出m的值,代入对应的式子求出n的值.
解答:解:(Ⅰ)令n=1代入an+1=
得,a2=a1+1=2,
令n=2代入得a3=a2+2=4;令n=3代入得a4=a3-3=1,
令n=4代入得a5=a4+4=5;
∴a1=1,a2=2,a3=4,a4=1,a5=5;
(Ⅱ)由(Ⅰ)可知n1=1,n2=4,n3=13,…,
猜想使ank=1的下标nk满足如下递推关系:nk+1=3nk+1,k=1,2,3,….
对k归纳:k=1,2时已成立,设已有ank=1,则由(Ⅰ)归纳可得,
ank+1=nk+1,ank+2=2nk+2,ank+3=nk,ank+4=2nk+3,….
归纳易得:ank+2m-1=nk+2-m,m=1,2,…,nk+1,ank+2m=2nk+1+m,m=1,2,…,nk,
故当m=nk+1时,a3nk+1=nk+2-(nk+1)=1=ank+1.
因此nk+1=3nk+1,(k=1,2,3,…)成立.
(Ⅲ)由(Ⅱ)可知,nk+1=3nk+1,则2nk+1=2(3nk+1),
即2nk+1+1=3(2nk+1),记2nk+1=xk,
则xk+1=3xk,x1=3,故xk=3k,因此nk=
,k=1,2,3,…,
由nk+1=3nk+1,k=1,2,3,…可知,
当n≤3nk=nk+1-1时,an≤3nk+1=nk+1.
因此,当n<n7时,an≤n7=
=1093;
而当n7≤n<n8时,要么有an≤1094,要么有an≥2×1094,即an取不到2013,
进而考虑n8≤n<n9的情况,
由(Ⅱ)得,ank+2m-1=nk+2-m,m=1,2,…,nk+1,
则n8+2-m=2013,解得m=1269,解得n8+2m-1=5817
故a5817=an8+2m-1=n8+2-m=2013.
故使得an=2013的最小n为5817.
|
令n=2代入得a3=a2+2=4;令n=3代入得a4=a3-3=1,
令n=4代入得a5=a4+4=5;
∴a1=1,a2=2,a3=4,a4=1,a5=5;
(Ⅱ)由(Ⅰ)可知n1=1,n2=4,n3=13,…,
猜想使ank=1的下标nk满足如下递推关系:nk+1=3nk+1,k=1,2,3,….
对k归纳:k=1,2时已成立,设已有ank=1,则由(Ⅰ)归纳可得,
ank+1=nk+1,ank+2=2nk+2,ank+3=nk,ank+4=2nk+3,….
归纳易得:ank+2m-1=nk+2-m,m=1,2,…,nk+1,ank+2m=2nk+1+m,m=1,2,…,nk,
故当m=nk+1时,a3nk+1=nk+2-(nk+1)=1=ank+1.
因此nk+1=3nk+1,(k=1,2,3,…)成立.
(Ⅲ)由(Ⅱ)可知,nk+1=3nk+1,则2nk+1=2(3nk+1),
即2nk+1+1=3(2nk+1),记2nk+1=xk,
则xk+1=3xk,x1=3,故xk=3k,因此nk=
| 3k-1 |
| 2 |
由nk+1=3nk+1,k=1,2,3,…可知,
当n≤3nk=nk+1-1时,an≤3nk+1=nk+1.
因此,当n<n7时,an≤n7=
| 37-1 |
| 2 |
而当n7≤n<n8时,要么有an≤1094,要么有an≥2×1094,即an取不到2013,
进而考虑n8≤n<n9的情况,
由(Ⅱ)得,ank+2m-1=nk+2-m,m=1,2,…,nk+1,
则n8+2-m=2013,解得m=1269,解得n8+2m-1=5817
故a5817=an8+2m-1=n8+2-m=2013.
故使得an=2013的最小n为5817.
点评:本题考查了利用数列的地推公式求数列中的项,再由归纳法得到有关项和项数之间的关系式,再通过赋值构造新的等比数列,考查了学生灵活应用能力和较强逻辑思维能力,难度很大.

练习册系列答案
相关题目
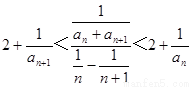 .
.