题目内容
15.已知等比数列{an}的第一项是$\frac{9}{8}$,最后一项是$\frac{1}{3}$.且各项的和是$\frac{65}{24}$.求:(1)这个等比数列的公比q;
(2)这个等比数列的通项公式.
分析 (1)根据条件建立方程关系即可求这个等比数列的公比q;
(2)根据等比数列的通项公式即可求这个等比数列的通项公式.
解答 解:∵等比数列{an}的第一项是$\frac{9}{8}$,最后一项是$\frac{1}{3}$.且各项的和是$\frac{65}{24}$.
∴$\frac{{a}_{1}(1-{q}^{n})}{1-q}$=$\frac{\frac{9}{8}(1-{q}^{n})}{1-q}$=$\frac{65}{24}$.
即65(1-q)=27(1-qn),①
∵an=a1qn-1,
∴$\frac{9}{8}$qn-1=$\frac{1}{3}$,即qn-1=$\frac{8}{27}$,
即qn=$\frac{8}{27}$q,代入①得65(1-q)=27(1-$\frac{8}{27}$q)=27-8q,
得57q=38,即q=$\frac{2}{3}$,则($\frac{2}{3}$)n-1=$\frac{8}{27}$=($\frac{2}{3}$)3,
即n-1=3,得n=4.
(2)∵q=$\frac{2}{3}$,a1=$\frac{9}{8}$,
∴an=($\frac{9}{8}$)•($\frac{2}{3}$)n-1=($\frac{3}{2}$)3•($\frac{2}{3}$)n-1=($\frac{2}{3}$)n-4.
点评 本题主要考查等比数列的通项公式以及等比数列的应用,根据条件建立方程关系是解决本题的关键.

练习册系列答案
相关题目
5.若程序框图如图所示,则该程序运行后输出k的值是( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
3.“α=$\frac{π}{4}$”是“tanα=1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
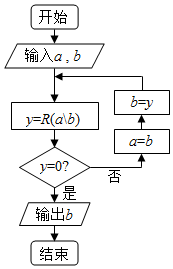 “辗转相除法”的算法思路如图所示,记R(a\b)为a除以b所得的余数(a,b∈N*),执行如图的程序框图,若输入a,b分别为405,75,则输出b的值为( )
“辗转相除法”的算法思路如图所示,记R(a\b)为a除以b所得的余数(a,b∈N*),执行如图的程序框图,若输入a,b分别为405,75,则输出b的值为( )