题目内容
19.已知函数f(x)=-x2+ax+b的值域为(-∞,0],若关x的不等式$f(x)>-\frac{c}{4}-1$的解集为(m-4,m+1),则实数c的值为21.分析 根据题意,△=a2+4b=0;m-4与m+1为方程x2-ax-b-$\frac{c}{4}$-1=0的两根;函数y=x2-ax-b-$\frac{c}{4}$-1的对称轴为x=$\frac{a}{2}$=$\frac{m+1-(m-4)}{2}$=$\frac{5}{2}$;可求出a,m的值,再求c.
解答 解:由题意,函数f(x)=-x2+ax+b的值域为(-∞,0],
∴△=a2+4b=0 ①;
由不等式$f(x)>-\frac{c}{4}-1$ 化简:x2-ax-b-$\frac{c}{4}$-1<0
m-4与m+1为方程x2-ax-b-$\frac{c}{4}$-1=0的两根;
m-4+m+1=a ②;
(m-4)(m+1)=-b-$\frac{c}{4}$-1 ③;
函数y=x2-ax-b-$\frac{c}{4}$-1的对称轴为x=$\frac{a}{2}$=$\frac{m+1-(m-4)}{2}$=$\frac{5}{2}$;
所以 a=5;
由①②知:m=4,b=-$\frac{25}{4}$;
由③知:c=21
故答案为:21
点评 本题主要考查了不等式方程组解与二次函数根的关系,以及二次函数的图形特征,属中等题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 用固定的速度向如图形状的瓶子中注水,则水面的高度h和时间t之间的关系可用图象大致表示为( )
用固定的速度向如图形状的瓶子中注水,则水面的高度h和时间t之间的关系可用图象大致表示为( )



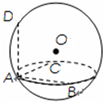 如图,设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且AB=AC=$\sqrt{6}$,AD=2,则球O的体积为$\frac{32π}{3}$.
如图,设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且AB=AC=$\sqrt{6}$,AD=2,则球O的体积为$\frac{32π}{3}$.